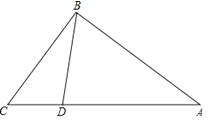
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动点A时停止,若设点D运动的时间为t秒,点D运动的速度为每秒2个单位长度.
(1)当t=2时,CD= ,AD= ;(请直接写出答案)
(2)当t= 时,△CBD是直角三角形;(请直接写出答案)
(3)求当t为何值时,△CBD是等腰三角形?并说明理由.
参考答案:
【答案】(1)4,21;(2)4.5或12.5秒;(3)t=6.25或7.5或9秒时,△CBD是等腰三角形.
【解析】试题分析:(1)根据CD=速度×时间列式计算即可得解,利用勾股定理列式求出AC,再根据AD=AC-CD代入数据进行计算即可得解;(2)分①∠CDB=90°时,利用△ABC的面积列式计算即可求出BD,然后利用勾股定理列式求解得到CD,再根据时间=路程÷速度计算;②∠CBD=90°时,点D和点A重合,然后根据时间=路程÷速度计算即可得解;(3)分①CD=BD时,过点D作DE⊥BC于E,根据等腰三角形三线合一的性质可得CE=BE,从而得到CD=AD;②CD=BC时,CD=6;③BD=BC时,过点B作BF⊥AC于F,根据等腰三角形三线合一的性质可得CD=2CF,再由(2)的结论解答.
试题解析:(1)t=2时,CD=2×2=4,
∵∠ABC=90°,AB=20,BC=15,
∴AC=![]() =25,
=25,
AD=ACCD=254=21;
(2)①∠CDB=90°时,S△ABC=![]() ACBD=
ACBD=![]() ABBC,
ABBC,
即![]() ×25BD=
×25BD=![]() ×20×15,
×20×15,
解得BD=12,
所以CD=![]() =9,
=9,
t=9÷2=4.5(秒);
②∠CBD=90°时,点D和点A重合,
t=25÷2=12.5(秒),
综上所述,t=4.5或12.5秒;
故答案为:(1)4,21;(2)4.5或12.5秒;
(3)①CD=BD时,如图1,

过点D作DE⊥BC于E,
则CE=BE,
CD=AD=![]() AC=
AC=![]() ×25=12.5,(或利用余角的性质说明CD=BD=AD)
×25=12.5,(或利用余角的性质说明CD=BD=AD)
t=12.5÷2=6.25;
②CD=BC时,CD=15,t=15÷2=7.5;
③BD=BC时,如图2,

过点B作BF⊥AC于F,
则CF=9,
CD=2CF=9×2=18,
t=18÷2=9,
综上所述,t=6.25或7.5或9秒时,△CBD是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】能把一个三角形分成两个面积相等的三角形是三角形的( )
A.中线
B.高线
C.角平分线
D.以上都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】判断下列命题是真命题还是假命题,如果是假命题,举出一个反例.
(1)等角的余角相等;
(2)平行线的同旁内角的平分线互相垂直;
(3)和为180°的两个角叫做邻补角. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)
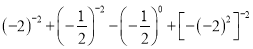
(2)
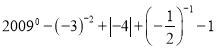
(3)
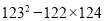 (4)
(4)
(5)
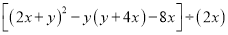 (6)
(6)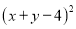
(7)
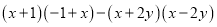
(8)
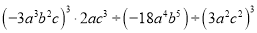
-
科目: 来源: 题型:
查看答案和解析>>【题目】阿里巴巴数据显示,2017年天猫商城“双11”全球狂欢交易额超1682亿元,数据1682亿用科学记数法表示为( )
A. 1682×108 B. 16.82×109 C. 1.682×1011 D. 0.1682×1012
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,能作为一个三角形的三边边长的是( )
A.1、2、4B.8、6、4、C.12、6、5D.3、3、6
-
科目: 来源: 题型:
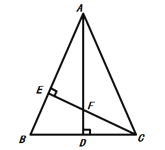
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE,求证:
(1)△AEF≌△CEB;
(2)AF=2CD。
相关试题

