【题目】求符合下列条件的抛物线的解析式:
(1)将抛物线y=-x2先向上平移1个单位长度,再绕其顶点旋转180°;
(2)抛物线y=ax2+1经过点(1,0);
(3)抛物线y=ax2-1与直线y=![]() x+3的一个交点是(2,m).
x+3的一个交点是(2,m).
参考答案:
【答案】 (1) y=x2+1;(2) y=-x2+1;(3) y=![]() x2-1.
x2-1.
【解析】试题分析:(1)根据抛物线的几何变换,抛物线y=-x2先向上平移1个单位长度,所得抛物线解析式为y=-x2+1,再绕其顶点旋转180°,与原抛物线的开口大小相等,方向相反时,顶点不变,其二次项系数互为相反数;
(2)把(1,0)代入解析式求出a即可;
(3)把x=2代入直线解析式y=![]() x+3,得y=4,因此交点坐标为(2,4),把(2,4)代入抛物线解析式,得a=
x+3,得y=4,因此交点坐标为(2,4),把(2,4)代入抛物线解析式,得a=![]() ,从而得到抛物线解析式.
,从而得到抛物线解析式.
试题解析:(1)抛物线y=-x2先向上平移1个单位长度,得y=-x2+1,
再绕其顶点旋转180°,得y=x2+1;
(2)把(1,0)代入直线解析式y=ax2+1,得a+1=0,解得a=-1,
所以抛物线的解析式为:y=-x2+1;
(3)把x=2代入直线解析式y=![]() x+3,
x+3,
得y=![]() ×2+3=4,
×2+3=4,
因此交点坐标为(2,4),
把(2,4)代入抛物线解析式,得4=a×22-1,a=![]() ,
,
所以抛物线解析式为:y=![]() x2-1.
x2-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】种植草莓大户张华现有22吨草莓等待出售,有两种销售渠道,一是运往省城直接批发给零售商,二是在本地市场零售,受客观因素影响,张华每天只能采用一种销售渠道,而且草莓必须在10天内售出(含10天)经过调查分析,这两种销售渠道每天销量及每吨所获纯利润见右表:
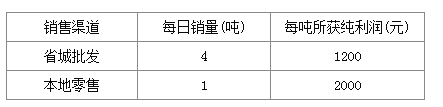
(1)若一部分草莓运往省城批发给零售商,其余在本地市场零售,请写出销售22吨草莓所获纯利润y(元)与运往省城直接批发零售商的草莓量x(吨)之间的函数关系式;
(2)怎样安排这22吨草莓的销售渠道,才使张华所获纯利润最大?并求出最大纯利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具厂有4个车间,某周是质量检查周,现每个车间都原有a(a>0)个成品,且每个车间每天都生产b(b>0)个成品,质量科派出若干名检验员周一、周二检验其中两个车间原有的和这两天生产的所有成品,然后,周三到周五检验另外两个车间原有的和本周生产的所有成品,假定每名检验员每天检验的成品数相同.
(1)这若干名检验员1天共检验多少个成品?(用含a、b的代数式表示)
(2)若一名检验员1天能检验
 b个成品,则质量科至少要派出多少名检验员?
b个成品,则质量科至少要派出多少名检验员? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图 (1),已知△ABC是等边三角形,以BC为直径的⊙O交AB、AC于D、E.求证:

(1)△DOE是等边三角形.
(2)如图(2),若∠A=60°,AB≠AC, 则(1)中结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标平面内,已点A(3,0)、B(-5,3),将点A向左平移6个单位到达C点,将点B向下平移6个单位到达D点.
(1)写出C点、D点的坐标:C __________,D ____________ ;
(2)把这些点按A-B-C-D-A顺次连接起来,这个图形的面积是__________.

相关试题

