【题目】甲、乙两车从A地出发沿同一路线驶向B地,甲车匀速驶向B地,甲车出发30分钟后,乙车才出发,乙先匀速行驶一段时间后,到达货站装货后继续行驶,速度减少了56千米/时,结果与甲车同时到达B地,甲乙两车距A地的路程y(千米)与乙车行驶时间x(时)之间的函数图象如图所示,下列说法中正确的是( ) 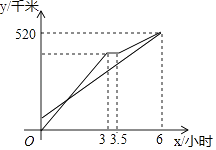
A.甲车从A地到B地行驶了6小时
B.甲的速度是120千米/时
C.乙出发90分钟追上甲
D.当两车在行驶过程中,相距40千米时,x=2或3.5
参考答案:
【答案】D
【解析】解:A、错误.甲车从A地到B地行驶了6.5小时. B、错误.甲的速度为 ![]() =80千米/时.
=80千米/时.
C、错误.设乙开始的速度为x千米/时,由题意3x+2.5(x﹣56)=520,解得x=120,
设乙出发t小时追上甲,则(120﹣80)t=0.5×80,t=1,
所以乙出发t小时追上甲.
D、正确.由题意甲的函数解析式为y=80x+40,
乙开始的函数解析式为y=120x,装货后的解析式为y=64x+136,
由题意120x﹣(80x+40)=40或64x+136﹣(80x+40)=40,
解得x=2或3.5.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设平面内一点到等边三角形中心的距离为d,等边三角形的内切圆半径为r,外接圆半径为R.对于一个点与等边三角形,给出如下定义:满足r≤d≤R的点叫做等边三角形的中心关联点. 在平面直角坐标系xOy中,等边△ABC的三个顶点的坐标分别为A(0,2),B(﹣
 ,﹣1),C(
,﹣1),C(  ,﹣1).
,﹣1).
(1)已知点D(2,2),E( ,1),F(﹣
,1),F(﹣  ,﹣1).在D,E,F中,是等边△ABC的中心关联点的是;
,﹣1).在D,E,F中,是等边△ABC的中心关联点的是;
(2)如图1,过点A作直线交x轴正半轴于M,使∠AMO=30°. ①若线段AM上存在等边△ABC的中心关联点P(m,n),求m的取值范围;
②将直线AM向下平移得到直线y=kx+b,当b满足什么条件时,直线y=kx+b上总存在等边△ABC的中心关联点;(直接写出答案,不需过程)
(3)如图2,点Q为直线y=﹣1上一动点,⊙Q的半径为 .当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.
.当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
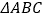 中,
中, 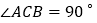 ,
, ,将
,将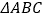 沿
沿 折叠,使点
折叠,使点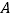 落在直角边
落在直角边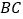 上的
上的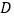 点处,设
点处,设 与
与 边分别交于点
边分别交于点 ,如果折叠后
,如果折叠后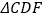 与
与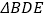 均为等腰三角形,那么
均为等腰三角形,那么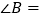 __________.
__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】AD是△ABC的高,AC=2
 ,AD=4,把△ADC沿着直线AD对折,点C落在点E的位置,如果△ABE是等腰三角形,那么线段BE的长度为( )
,AD=4,把△ADC沿着直线AD对折,点C落在点E的位置,如果△ABE是等腰三角形,那么线段BE的长度为( )
A.2
B.2 或5
或5
C.2
D.5 -
科目: 来源: 题型:
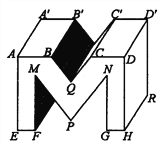
查看答案和解析>>【题目】如图所示,在书写艺术字时,常常运用画“平行线段”这种基本作图方法,此图是在书写字“M”:
(1)请从正面,上面,右侧三个不同方向上各找出一组平行线段,并用字母表示出来;
(2)EF与A′B′有何位置关系?CC′与DH有何位置关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,P是BC上一点,E是AB上一点,PD平分∠APC,PE⊥PD,连接DE交AP于F,在以下判断中,不正确的是( )

A.当P为BC中点,△APD是等边三角形
B.当△ADE∽△BPE时,P为BC中点
C.当AE=2BE时,AP⊥DE
D.当△APD是等边三角形时,BE+CD=DE -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平面直角坐标系中,
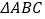 的顶点
的顶点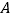 的坐标为
的坐标为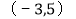 ,顶点
,顶点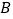 的坐标为
的坐标为 ,顶点
,顶点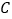 的坐标为
的坐标为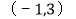 .
.(1)请你在所给的平面直角坐标系中,画出
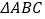 关于
关于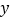 轴对称的
轴对称的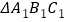 ;
;(2)将(1)中得到的
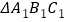 向下移动4个单位得到
向下移动4个单位得到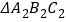 ,画出
,画出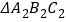 ;
;(3)在
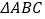 中有一点
中有一点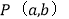 ,直接写出经过以上两次图形变换后
,直接写出经过以上两次图形变换后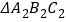 中对应点
中对应点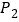 的坐标.
的坐标.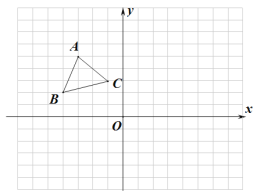
相关试题

