Question

【题目】在平面直角坐标系xOy中，抛物线y=ax2+bx+2过B（﹣2，6），C（2，2）两点．

（1）记抛物线顶点为D，求△BCD的面积；

（2）若直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC（包括端点B、C）部分有两个交点，求b的取值范围．

Answer 1

【答案】（1）3 （2）＜b≤3．

【解析】（1）根据待定系数法即可解决问题．求出直线BC与对称轴的交点H，根据S△BDC=S△BDH+S△DHC即可解决问题．

（2）由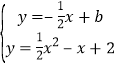，当方程组只有一组解时求出b的值，当直线y=﹣x+b经过点C时，求出b的值，当直线y=﹣x+b经过点B时，求出b的值，由此即可解决问题．

解：（1）由题意解得，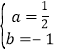

∴抛物线解析式为y=x2﹣x+2．

∵y=x2﹣x+2=（x﹣1）2+．

∴顶点坐标（1，），

∵直线BC为y=﹣x+4，∴对称轴与BC的交点H（1，3），

∴S△BDC=S△BDH+S△DHC=×（3-）3+×（3-）1=3．

（2）由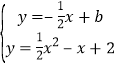消去y得到x2﹣x+4﹣2b=0，

当△=0时，直线与抛物线相切，1﹣4（4﹣2b）=0，

∴b=，

当直线y=﹣x+b经过点C时，b=3，

当直线y=﹣x+b经过点B时，b=5，

∵直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC（包括端点B、C）部分有两个交点，

∴＜b≤3．

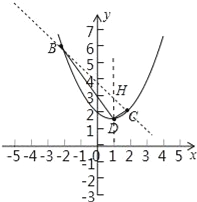
“点睛”本题考查待定系数法确定二次函数解析式、二次函数性质等知识，解题的关键是求出对称轴与直线BC交点H坐标，学会利用判别式确定两个函数图象的交点问题，属于中考常考题型．