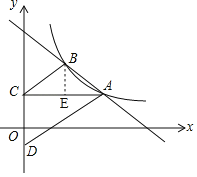
【题目】如图,在平面直角坐标系中,直线AB与函数y=![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.
(1)求m,k,n的值;
(2)求△ABC的面积.

参考答案:
【答案】(1) m=4,k=8,n=4;(2)△ABC的面积为4.
【解析】试题分析:(1)由点A的纵坐标为2知OC=2,由OD=![]() OC知OD=1、CD=3,根据△ACD的面积为6求得m=4,将A的坐标代入函数解析式求得k,将点B坐标代入函数解析式求得n;
OC知OD=1、CD=3,根据△ACD的面积为6求得m=4,将A的坐标代入函数解析式求得k,将点B坐标代入函数解析式求得n;
(2)作BE⊥AC,得BE=2,根据三角形面积公式求解可得.
试题解析:(1)∵点A的坐标为(m,2),AC平行于x轴,
∴OC=2,AC⊥y轴,
∵OD=OC,
∴OD=1,
∴CD=3,
∵△ACD的面积为6,
∴![]() CDAC=6,
CDAC=6,
∴AC=4,即m=4,
则点A的坐标为(4,2),将其代入y=![]() 可得k=8,
可得k=8,
∵点B(2,n)在y=![]() 的图象上,
的图象上,
∴n=4;
(2)如图,过点B作BE⊥AC于点E,则BE=2,
∴S△ABC=![]() ACBE=
ACBE=![]() ×4×2=4,
×4×2=4,
即△ABC的面积为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)问题
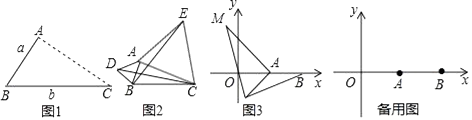
如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于时,线段AC的长取得最大值,且最大值为(用含a,b的式子表示)
(2)应用
点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90,请直接写出线段AM长的最大值及此时点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】P(2m-4,1-2m)在y轴上,则m=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】上周六上午
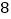 点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离
点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离  (千米)与他们路途所用的时间
(千米)与他们路途所用的时间  (时)之间的函数图象,请根据以上信息,解答下列问题:
(时)之间的函数图象,请根据以上信息,解答下列问题:
(1)求直线 所对应的函数关系式;
所对应的函数关系式;
(2)已知小颖一家出服务区后,行驶 分钟时,距姥姥家还有
分钟时,距姥姥家还有  千米,问小颖一家当天几点到达姥姥家?
千米,问小颖一家当天几点到达姥姥家? -
科目: 来源: 题型:
查看答案和解析>>【题目】在我们常见的英文字母中,存在着同位角、内错角、同旁内角的现象.在下列几个字母中,不含同旁内角现象的字母是( )
A.E
B.F
C.N
D.H -
科目: 来源: 题型:
查看答案和解析>>【题目】某旅游景点的门票售价为:成人票每张50元,儿童票每张30元,如果某日该景点售出门票100张,门票收入共4000元,那么当日售出成人票张.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用二元一次方程组解应用题:甲、乙两地相距
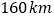 ,一辆汽车和一辆拖拉机同时由两地以各自的速度匀速相向而行,
,一辆汽车和一辆拖拉机同时由两地以各自的速度匀速相向而行, 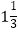 小时后相遇.相遇后,拖拉机以其原速继续前进,汽车在相遇处停留
小时后相遇.相遇后,拖拉机以其原速继续前进,汽车在相遇处停留 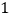 小时后调转车头以其原速返回,在汽车再次出发半小时追上拖拉机.这时,汽车、拖拉机各自走了多少路程?
小时后调转车头以其原速返回,在汽车再次出发半小时追上拖拉机.这时,汽车、拖拉机各自走了多少路程?
相关试题

