【题目】如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为 . 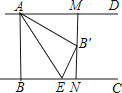
参考答案:
【答案】![]() 或
或 ![]()
![]()
【解析】解:如图 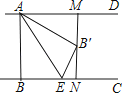 ,
,
由翻折的性质,得
AB=AB′,BE=B′E.
①当MB′=2,B′N=1时,设EN=x,得
B′E= ![]() .
.
△B′EN∽△AB′M,![]() ,即
,即 ![]() =
= ![]() ,x2=
,x2= ![]() ,BE=B′E=
,BE=B′E= ![]() =
= ![]() .
.
②当MB′=1,B′N=2时,设EN=x,得
B′E= ![]() ,
,
△B′EN∽△AB′M,![]() ,即
,即 ![]() =
= ![]() ,解得x2=
,解得x2= ![]() ,BE=B′E=
,BE=B′E= ![]() =
= ![]() ,
,
故答案为: ![]() 或
或 ![]() .
.
根据勾股定理,可得EB′,根据相似三角形的性质,可得EN的长,根据勾股定理,可得答案.本题考查了翻折的性质,利用翻折的性质得出AB=AB′,BE=B′E是解题关键,又利用了相似三角形的性质,要分类讨论,以防遗漏.
-
科目: 来源: 题型:
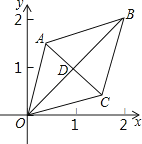
查看答案和解析>>【题目】如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为( )
A.(1,﹣1)
B.(﹣1,﹣1)
C.(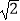 ,0)
,0)
D.(0,﹣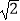 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作
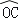 交
交 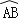 于点C,若OA=2,则阴影部分的面积为 .
于点C,若OA=2,则阴影部分的面积为 . 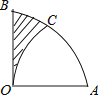
-
科目: 来源: 题型:
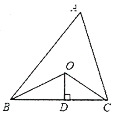
查看答案和解析>>【题目】如图,已知△ABC的周长是16,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D且OD=2,△ABC的面积是________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
( ﹣1)÷
﹣1)÷ 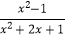 ,其中x的值从不等式组
,其中x的值从不等式组 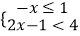 的整数解中选取.
的整数解中选取. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出下列四个结论:
①AE=CF;
②△EPF是等腰直角三角形;
③EF=AB;
④
 ,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有________(把你认为正确的结论的序号都填上).
,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有________(把你认为正确的结论的序号都填上).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640
6430
6520
6798
7325
8430
8215
7453
7446
6754
7638
6834
7326
6830
8648
8753
9450
9865
7290
7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表组别
步数分组
频数
A
5500≤x<6500
2
B
6500≤x<7500
10
C
7500≤x<8500
m
D
8500≤x<9500
3
E
9500≤x<10500
n
请根据以上信息解答下列问题:
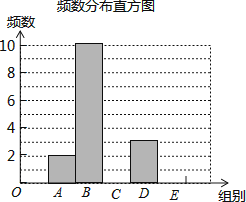
(1)填空:m= , n=
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在组;
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
相关试题

