搜索
【题目】ABC与DEF的相似比为1：3，则ABC与DEF的面积比为（ ）
A. 1：3 B. 1：6 C. 1：9 D. 1：16
参考答案：
【答案】C
【解析】由相似△ABC与△DEF的相似比为1：3，根据相似三角形面积的比等于相似比的平方，即可求得△ABC与△DEF的面积比．
∵相似△ABC与△DEF的相似比为1：3，
∴△ABC与△DEF的面积比为1：9．
故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】方程(x+1)(x－2)=x+1的解是（ ）
A. 2 B. 3 C. －1，2 D. －1，3
-
科目： 来源： 题型：
查看答案和解析>>【题目】用一根长为24 cm的铁丝围成一个长与宽的比是2∶1的长方形，则长方形的面积是( )．
A. 32 cm2 B. 36 cm2 C. 144 cm2 D. 以上都不对
-
科目： 来源： 题型：
查看答案和解析>>【题目】直线 y 2x 6 与 x 轴的交点坐标是______________。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，延长BC至点F，使CF=
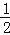BC，连接CD和EF．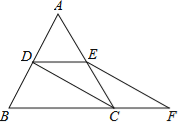
（1）求证：DE=CF；
（2）求EF的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠DCO.
-
科目： 来源： 题型：
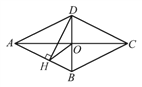
查看答案和解析>>【题目】（1）如图①，直线AB∥CD，E是AB与AD之间的一点，连接BE，CE，可以发现∠B+∠C=∠BEC．
证明过程如下：
证明：过点E作EF∥AB，
∵AB∥DC，EF∥AB（辅助线的作法），
∴EF∥DC
∴∠C=∠CEF．
∵EF∥AB，∴∠B=∠BEF
∴∠B+∠C=∠CEF+∠BEF
即∠B+∠C=∠BEC．
（2）如果点E运动到图②所示的位置，其他条件不变，∠B，∠C，∠BEC又有什么关系？并证明你的结论；
（3）如图③，AB∥DC，∠C=120°，∠AEC=80°，则∠A= ．（写出结论，不用写计算过程）。
相关试题
