【题目】在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE,BE分别交于点G、H.∠CBE=∠BAD,有下列结论:①FD=FE;②AH=2CD;③BCAD=![]() AE2;④S△BEC=S△ADF.其中正确的有( )
AE2;④S△BEC=S△ADF.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】
根据题意和图形,可以判断各小题中的结论是否成立,从而可以解答本题.
∵在△ABC中,AD和BE是高,
∴∠ADB=∠AEB=∠CEB=90°,
∵点F是AB的中点,
∴FD=![]() AB,FE=
AB,FE=![]() AB,
AB,
∴FD=FE,①正确;
∵∠CBE=∠BAD,∠CBE+∠C=90°,∠BAD+∠ABC=90°,
∴∠ABC=∠C,
∴AB=AC,
∵AD⊥BC,
∴BC=2CD,∠BAD=∠CAD=∠CBE,
在△AEH和△BEC中, ,
,
∴△AEH≌△BEC(ASA),
∴AH=BC=2CD,②正确;
∵∠BAD=∠CBE,∠ADB=∠CEB,
∴△ABD∽△BCE,
∴![]() ,即BCAD=ABBE,
,即BCAD=ABBE,
∵∠AEB=90°,AE=BE,
∴AB=![]() BE
BE
BCAD=![]() BEBE,
BEBE,
∴BCAD=![]() AE2;③正确;
AE2;③正确;
设AE=a,则AB=![]() a,
a,
∴CE=![]() a﹣a,
a﹣a,
∴ =
=![]() ,
,
即![]() ,
,
∵AF=![]() AB,
AB,
∴ ![]() ,
,
∴S△BEC≠S△ADF,故④错误,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C为⊙O上一点,AD⊥CD,(点D在⊙O外)AC平分∠BAD.
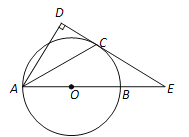
(1)求证:CD是⊙O的切线;
(2)若DC、AB的延长线相交于点E,且DE=12,AD=9,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE,易证△BCE≌△ACD.则
①∠BEC=______°;②线段AD、BE之间的数量关系是______.
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.

(3)探究发现:
如图3,P为等边△ABC内一点,且∠APC=150°,且∠APD=30°,AP=5,CP=4,DP=8,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,直线
 与x轴、y轴分别交于点A、C两点,点B的横坐标为2.
与x轴、y轴分别交于点A、C两点,点B的横坐标为2.
图1 图2
(1)求A、C两点的坐标和抛物线的函数关系式;
(2)点D是直线AC上方抛物线上任意一点,P为线段AC上一点,且S△PCD=2S△PAD ,求点P的坐标;
(3)如图2,另有一条直线y=-x与直线AC交于点M,N为线段OA上一点,∠AMN=∠AOM.点Q为x轴负半轴上一点,且点Q到直线MN和直线MO的距离相等,求点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,反比例函数y=
 (x>0)的图象交矩形OABC的边AB于点D,交BC于点E,且BE=2EC,若四边形ODBE的面积为8,则k=_____.
(x>0)的图象交矩形OABC的边AB于点D,交BC于点E,且BE=2EC,若四边形ODBE的面积为8,则k=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图在ABCD中,点E为AB上一点,连接CE、DE,且CE⊥AB,CE=AB,点F为BC上一点,连接DF交CE于点G,∠CGD=∠B;

(1)若CG=2,AD=3,求GE的长;
(2)若CF=
 DE,求证:AD=CG+BE.
DE,求证:AD=CG+BE. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠ABC=60°,AB=6cm,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的点D处,则AC边扫过的图形(阴影部分)的面积是_____cm2.(结果保留π).

相关试题

