搜索
【题目】如图，二次函数y=﹣
x2+bx+c的图象经过A（2，0），B（0，﹣6）两点，
（1）求这个二次函数的解析式；
（2）设该二次函数的对称轴与x轴交于点C，连接BA，BC，求△ABC的面积．
参考答案：
【答案】（1）这个二次函数的解析式为y=﹣
x2+4x﹣6；（2）S△ABC=6．
【解析】试题分析：（1）二次函数图象经过A（2，0）、B（0，﹣6）两点，两点代入y=
+bx+c，算出b和c，即可得解析式．
（2）先求出对称轴方程，写出C点的坐标，计算出AC，然后由面积公式计算值．
试题解析：（1）把A（2，0）、B（0，﹣6）代入y=+bx+c，
得：
，
解得
，
∴这个二次函数的解析式为y=+4x﹣6；
（2）∵该抛物线对称轴为直线x=
=4，
∴点C的坐标为（4，0），
∴AC=OC﹣OA=4﹣2=2，
∴
=×AC×OB=×2×6=6．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某景区一电瓶小客车接到任务从景区大门出发，向东走2千米到达A景区，继续向东走2.5千米到达B景区，然后又回头向西走8.5千米到达C景区，最后回到景区大门．
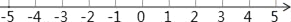
（1）以景区大门为原点，向东为正方向，以1个单位长表示1千米，建立如图所示的数轴，请在数轴上表示出上述A、B、C三个景区的位置．
（2）若电瓶车充足一次电能行走15千米，则该电瓶车能否在一开始充好电而途中不充电的情况下完成此次任务？请计算说明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示．在△ABC中，∠ACB=90°，AC=BC，过点C任作一直线PQ，过点A作
于点M，过点B作BN
PQ于点N．
（1）如图①，当M、N在△ABC的外部时，MN、AM、BN有什么关系呢？为什么？
（2）如图②，当M、N在△ABC的内部时，（1）中的结论是否仍然成立？若成立，请说明理由；若不成立，请指出MN与AM、BN之间的数关系并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是某种产品展开图，高为3cm.
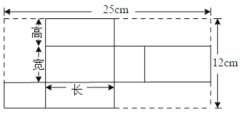
（1）求这个产品的体积.
（2）请为厂家设计一种包装纸箱，使每箱能装5件这种产品，要求没有空隙且要使该纸箱所用材料尽可能少（纸的厚度不计，纸箱的表面积尽可能小），求此长方体的表面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是
A．AB∥DC，AD∥BC B．AB=DC，AD=BC
C．AO=CO，BO=DO D．AB∥DC，AD=BC
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，小明用三个等腰三角形（图中①②③）拼成了一个平行四边形ABCD，且
，则
=_____ 度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】现场学习题：
问题背景：
在△ABC中，AB、BC、AC三边的长分别为
、
、
，求这个三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示，这样不需求△ABC的高，而借用网格就能计算出它的面积．
（1）请你将△ABC的面积直接填写在横线上． ．
思维拓展：
（2）我们把上述求△ABC面积的方法叫做构图法，若△ABC三边的长分别为
a，2
a、
a（a＞0），请利用图2的正方形网格（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积是： ．探索创新：
（3）若△ABC三边的长分别为
、
、
（m＞0，n＞0，m≠n），请运用构图法在图3指定区域内画出示意图，并求出△ABC的面积为： ．
相关试题
