【题目】如图,O是直线AB上的一点,OC⊥OD,垂足为O.
(1)若∠BOD=32°,求∠AOC的度数;
(2)若∠AOC:∠BOD=2:1,直接写出∠BOD的度数.
参考答案:
【答案】
(1)
解:∵OC⊥OD
∴∠COD=90°
∵∠AOB是平角
∴∠AOB=180°
∵∠BOD=32°
∴∠AOC=180°-∠BOD-∠COD=58°
(2)
解:设∠BOD=x,则∠AOC=2x,
∴x+2x+90°=180°,
∴x=30°,
即∠BOD=30°.
【解析】(1)根据OC⊥OD可得∠COD=90°,再由∠AOB为平角,∠BOD=32°即可求得∠AOC的度数;
(2)设∠BOD=x,则∠AOC=2x,根据平角的定义列方程x+2x+90°=180°,求解即可.
【考点精析】本题主要考查了角的运算和垂线的性质的相关知识点,需要掌握角之间可以进行加减运算;一个角可以用其他角的和或差来表示;垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的每个内角都为108°,则它的边数为( )
A.5
B.8
C.6
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为54°,已知坡角为30°,求楼房AB的高度。(tan54°≈1.38,结果精确到0.1m)
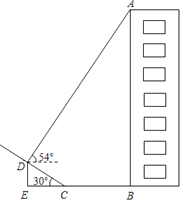
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.
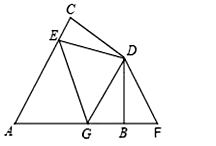
(1)试说明:DE=DF;
(2)在图中,若G在AB上且∠EDG=60°,试猜想CE、EG、BG之间的数量关系并证明此结论;
(3)若题中条件“∠CAB=60°,∠CDB=120°”改为∠CAB=α,∠CDB=180°-α,G在AB上,∠EDG满足什么条件时,(2)中结论仍然成立?(只写结果不要证明). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a<0,则点P(﹣a2 , ﹣a+1)关于原点的对称点P′在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形ABCD中,AD∥BC,AD=3cm,BC=7cm,∠B=60°,P为下底BC边上一点(不与B、C重合),连结AP,过P点作PE交DC于E,使得∠APE=∠B.
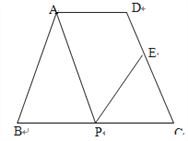
(1)求证:△ABP∽△PCE;
(2)求腰AB的长;
(3)在底边BC上是否存在一点P,使得DE:EC=5:3.如果存在,求出BP的长;如果不存在,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a+2a=3a2B. 3a﹣2a=a
C. a2a3=a6D. 6a2÷2a2=3a2
相关试题

