【题目】四张小卡片上分别写有数字1、2、3、4。它们除数字外没有任何区别,现将它们放在盒子里搅匀.
(1)随机地从盒子里抽取一张,求抽到数字2的概率.
(2)随机地从盒子里抽取一张,记下数字后放回再抽取第二张。请你用画树状图或列表的方法表示所有等可能的结果,并求抽到的数字之和为5的概率.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析: (1)随机地从盒子里抽取一张,共有4种等可能的结果,而抽到数字2的占1种,利用概率公式即可求得抽到数字2的概率;
(2)利用列表法展示所有16种等可能的结果,其中抽到的数字之和为5占4种,利用概率公式即可求得抽到的数字之和为5的概率.
试题解析:
解:(1)四张卡片中,只有1张写有数字2,故随机地从盒子里抽取一张,求抽到数字2的概率为![]() .
.
(2)根据题意列表,如图所示.由图可知,共有16种等可能的结果,数字之和为5的结果有4种,故数字之和为5的概率为![]() .
.
结果 | 1 | 2 | 3 | 4 |
1 | (1,1) | (1,2) | (1,3) | (1,4) |
2 | (2,1) | (2,2) | (2,3) | (2,4) |
3 | (3,1) | (3,2) | (3,3) | (3,4) |
4 | (4,1) | (4,2) | (4,3) | (4,4) |
-
科目: 来源: 题型:
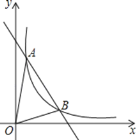
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数
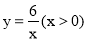 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.(1)求一次函数的解析式;
(2)根据图象直接写出
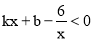 的x的取值范围;
的x的取值范围;(3)求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
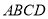 中,沿着直线
中,沿着直线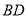 折叠,使点
折叠,使点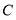 落在
落在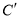 处,
处,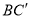 交
交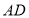 于
于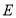 ,
,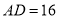 ,
,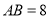 ,则
,则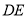 的长是____.
的长是____.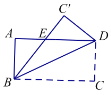
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平安路与幸福路是两条平行的道路,且与新兴大街垂直,老街与小米胡同垂直,书店位于老街与小米胡同的交口处,如果小强同学站在平安路与新兴大街的交叉路口,准备去书店,按图中的街道行走,最近的路程为____________ m.
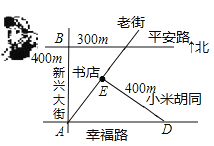
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一节数学课上,老师布置了一个任务:
已知,如图1,在
 中,
中, ,用尺规作图作矩形
,用尺规作图作矩形 .
.

同学们开动脑筋,想出了很多办法,其中小亮作了图2,他向同学们分享了作法:
①分别以点
 、
、 为圆心,大于
为圆心,大于 长为半径画弧,两弧分别交于点
长为半径画弧,两弧分别交于点 、
、 ,连接
,连接 交
交 于点
于点 ;
;②作射线
 ,在
,在 上取点
上取点 ,使
,使 ;
;③连接
 ,
, .
.则四边形
 就是所求作的矩形.
就是所求作的矩形.老师说:“小亮的作法正确.”
写出小亮的作图依据.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用勾股定理可以在数轴上画出表示
 的点,请依据以下思路完成画图,并保留画图痕迹:
的点,请依据以下思路完成画图,并保留画图痕迹:
第一步:(计算)尝试满足
 ,使其中
,使其中 ,
,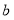 都为正整数.你取的正整数
都为正整数.你取的正整数 _____,
_____, _____;
_____;第二步:(画长为
 的线段)以第一步中你所取的正整数
的线段)以第一步中你所取的正整数 ,
,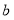 为两条直角边长画
为两条直角边长画 ,使
,使 为原点,点
为原点,点 落在数轴的正半轴上,
落在数轴的正半轴上, ,则斜边
,则斜边 的长即为
的长即为 .
.请在下面的数轴上画图:(第二步不要求尺规作图,不要求写画法)
第三步:(画表示
 的点)在下面的数轴上画出表示
的点)在下面的数轴上画出表示 的点
的点 ,并描述第三步的画图步骤:__________________.
,并描述第三步的画图步骤:__________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)直角三角形有一个非常重要的性质质:直角三角形斜边上的中线等于斜边的一半,比如:如图1,Rt△ABC中,∠C=90°,D为斜边AB中点,则CD=AD=BD=-AB.请你利用该定理和以前学过的知识解决下列问题:
在△ABC中,直线
 绕顶点A旋转.
绕顶点A旋转.(1)如图2,若点P为BC边的中点,点B、P在直线
 的异侧,BM⊥直线
的异侧,BM⊥直线 于点M,CN⊥直线
于点M,CN⊥直线 于点N,连接PM、PN.求证:PM=PN;
于点N,连接PM、PN.求证:PM=PN;(2)如图3,若点B、P在直线
 的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;(3)如图4,∠BAC=90°,直线
 旋转到与BC垂直的位置,E为AB上一点且AE=AC,EN⊥
旋转到与BC垂直的位置,E为AB上一点且AE=AC,EN⊥ 于N,连接EC,取EC中点P,连接PM、PN,求证:PM⊥PN.
于N,连接EC,取EC中点P,连接PM、PN,求证:PM⊥PN.
相关试题

