搜索
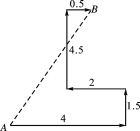
【题目】如图，某人到岛上去探宝，从A处登陆后先往东走4 km，又往北走1.5 km，遇到障碍后又往西走2 km，再折回向北走到4.5 km处往东一拐，仅走0.5 km就找到宝藏．问登陆点A与宝藏埋藏点B之间的距离是多少？
参考答案：
【答案】登陆点A与宝藏埋藏点B之间的距离是6.5 km.
【解析】
过点B作BC⊥AD于点C,根据题意可得AC＝4－2＋0.5＝2.5(km),BC＝4.5＋1.5＝6(km),然后根据勾股定理可得AB2＝AC2＋BC2＝2.52＋62＝6.52,继而求出AB.
解:如图,过点B作BC⊥AD于点C,
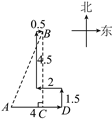
则AC＝4－2＋0.5＝2.5(km),BC＝4.5＋1.5＝6(km),
在Rt△ABC中,由勾股定理,得:
AB2＝AC2＋BC2＝2.52＋62＝6.52,
∴AB＝6.5(km)．
答:登陆点A与宝藏埋藏点B之间的距离是6.5 km.
-
科目： 来源： 题型：
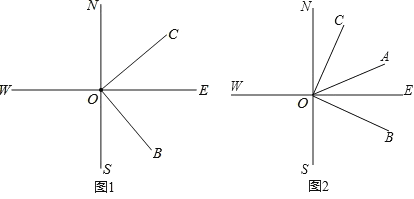
查看答案和解析>>【题目】如图1，直线SN与直线WE相交于点O，射线ON表示正北方向，射线OE表示正东方向，已知射线OB的方向是南偏东m°，射线OC的方向为北偏东n°，且m°的角与n°的角互余．
（1）①若m=60，写出射线OC的方向．（直接回答）
②请直接写出图中所有与∠BOE互余的角及与∠BOE互补的角．
（2）如图2，若射线OA是∠BON的平分线，
①若m=70，求∠AOC的度数．
②若m为任意角度，求∠AOC的度数．（结果用含m的式子表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以O为圆心，任意长为半径画弧，与射线OM交于点A，再以A为圆心，AO长为半径画弧，两弧交于点B，画射线OB，则sin∠AOB的值等于（ ）
A.
B.
C.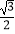
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，直线MN是等边△ABC底边BC的中垂线，点P在直线MN上，且使△PAB、△PAC、△PBC都是等腰三角形，满足上述条件的点P的个数有（ ）
A.1个
B.2个
C.3个
D.4个 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，PE，PF分别交AB，AC于点E，F，给出下列四个结论：①△APE≌△CPF；②AE=CF；③△EAF是等腰直角三角形；④S△ABC=2S四边形AEPF，上述结论正确的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】①在数轴上没有点能表示
+1；②无理数是开不尽方的数；③存在最小的实数；④4的平方根是±2，用式子表示是
=±2；⑤某数的绝对值，相反数，算术平方根都是它本身，则这个数是0，其中正确的是______． -
科目： 来源： 题型：
查看答案和解析>>【题目】元旦晚会上，王老师要为她的学生及班级的六位科任老师送上贺年卡，网上购买贺年卡的优惠条件是：购买50或50张以上享受团购价．王老师发现：零售价与团购价的比是5：4，王老师计算了一下，按计划购买贺年卡只能享受零售价，如果比原计划多购买6张贺年卡就能享受团购价，这样她正好花了100元，而且比原计划还节约10元钱；
（1）贺年卡的零售价是多少？
（2）班里有多少学生？
相关试题
