【题目】在平面直角坐标系中,已知A(a,b),B(2,2),且|a-b+8|+![]() =0.
=0.
(1)求点A的坐标;
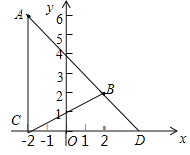
(2)过点A作AC⊥x轴于点C,连接BC,AB,延长AB交x轴于点D,设AB交y轴于点E,那么OD与OE是否相等?请说明理由.
(3)在x轴上是否存在点P,使S△OBP=S△BCD?若存在,请求出P点坐标,若不存在,请说明理由.
参考答案:
【答案】(1)点A的坐标为(-2,6);(2)OD与OE相等.理由见解析;(3)存在. P(-6,0)或(6,0).
【解析】
(1)利用非负数的性质解决问题即可.
(2)如图2,OD与OE相等.通过计算证明OE=4,OD=4即可解决问题.
(3)假设存在.设P(m,0),构建方程求出m即可解决问题.
(1)由|a-b+8|+![]() =0,
=0,
![]() ,
,
解得:![]() .
.
∴点A的坐标为(-2,6);
(2)如图2,OD与OE相等.理由如下:
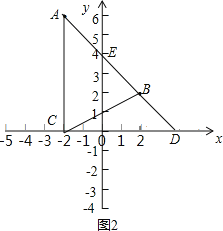
设点D的坐标为(x,0)(x>0),点E的坐标为(0,y)(y>0),
则CD=x+2,OE=y,
因为,三角形ABC的面积=三角形ACD的面积-三角形BCD的面积,
所以,12=![]() ×(x+2)×6-
×(x+2)×6-![]() ×(x+2)×2=2(x+2),
×(x+2)×2=2(x+2),
解得,x=4,即OD=4.
又因为,三角形EOD的面积=三角形ACD的面积-梯形ACOE的面积,
所以,![]() ×4×y=
×4×y=![]() ×6×6-
×6×6-![]() ×(y+6)×2,
×(y+6)×2,
解得:y=4,即OE=4,
所以,OD=OE.
(3)存在.设P(m,0),
由题意:![]() |m|×2=6,
|m|×2=6,
解得m=±6,
∴P(-6,0)或(6,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,CD是边AB上的高,且
 .
.(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.

-
科目: 来源: 题型:
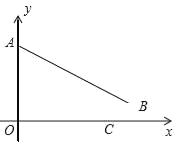
查看答案和解析>>【题目】如图平面直角坐标系中,已知三点 A(0,7),B(8,1),C(x,0)且 0<x <8.
(1)求线段 AB 的长;
(2)请用含 x 的代数式表示 AC+BC 的值;
(3)求 AC+BC 的最小值.
-
科目: 来源: 题型:
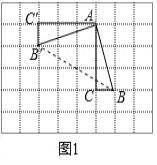
查看答案和解析>>【题目】(1)(操作发现)
如图 1,在边长为 1 个单位长度的小正方形组成的网格中,ABC 的三个顶点均在格点上.现将ABC 绕点 A 按顺时针方向旋转 90°,点 B 的对应点为 B′,点 C 的对应点为 C′, 连接 BB′,如图所示则∠AB′B= .
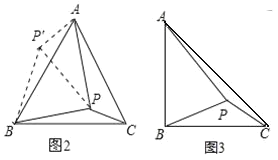
(2)(解决问题)
如图 2,在等边ABC 内有一点 P,且 PA=2,PB=
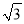 ,PC=1,如果将△BPC 绕点 B 顺时针旋转 60°得出△ABP′,求∠BPC 的度数和 PP′的长;
,PC=1,如果将△BPC 绕点 B 顺时针旋转 60°得出△ABP′,求∠BPC 的度数和 PP′的长;(3)(灵活运用)
如图 3,将(2)题中“在等边ABC 内有一点 P 改为“在等腰直角三角形 ABC 内有一点P”,且 BA=BC,PA=6,BP=4,PC=2,求∠BPC 的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄
清理养鱼网箱人数/人
清理捕鱼网箱人数/人
总支出/元
A
15
9
57000
B
10
16
68000
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,M 为 EF 中点,则 AM 的最小值为( )
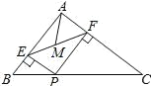
A.1B.1.3C.1.2D.1.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择了一点B(点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸).
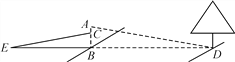
①小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面的距离AB=1.7米;
②小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6米,小明的眼睛距地面的距离CB=1.2米.
根据以上测量过程及测量数据,请你求出河宽BD是多少米?
相关试题

