【题目】某店每天卖出300只粽子,卖出一只粽子的得润为1元。经调查发现,零售单价每降0.1元,每天可多卖出100只粽子。为了使每天获得的利润更多,该店决定把零售单价下降m(0<m<1)元.
(1)零售单价降价后,该店每天可售出 只粽子,利润为 元。
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元,且卖出的粽子更多?
参考答案:
【答案】(1)![]() ,
,![]() ;(2)0.4
;(2)0.4
【解析】(1)每天的销售量等于原有销售量加上增加的销售量即可;利润等于销售量乘以单价即可得到;(2)利用总利润等于销售量乘以每件的利润即可得到方程求解,并根据题中要求即可得到答案.
解:(1)![]() ,
,![]()
(2)根据题意,得![]() ,
,
解得![]() ,
,
当![]() ,
,![]() ,
,
当![]() 时,
时,![]()
∵700>600,
∴取![]()
答:当零售单价下降0.4元时,才能使该店每天获取的利润是420元,且卖出的粽子更多.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点A的坐标为(2,1),正比例函数y=kx的图象与线段OA的夹角是45°,求这个正比例函数的表达式为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果(a+b)2﹣(a﹣b)2=4,则一定成立的是( )
A. a是b的相反数B. a是﹣b的相反数
C. a是b的倒数D. a是﹣b的倒数
-
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发型了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQO使得∠O=90°,点Q在在直角坐标系y轴正半轴上,点P在x轴正半轴上,点O与原点重合,∠OQP=60°,点H在边QO上,点D、E在边PO上,点G、F在边PQ上,那么点P坐标为___________.
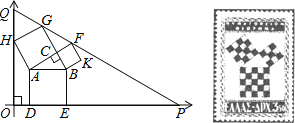
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=2x2﹣4x﹣4的顶点坐标是( )
A. (1,﹣6)B. (1,﹣4)C. (﹣3,﹣6)D. (﹣3,﹣4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,
连接AD,BC,BD.
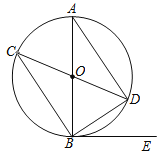
(1)求证:△ABD≌△CDB;
(2)若∠DBE=35°,求∠ADC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(0,4)是直角坐标系y轴上一点,动点P从原点O出发,沿x轴正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.
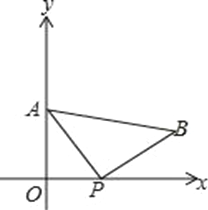
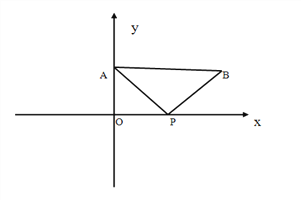
(1)若AB//x轴,如图一,求t的值;
(2)当t=3时,坐标平面内有一点M(不与A重合),使得以M、P、B为顶点的三角形和△ABP全等,请直接写出点M的坐标;
(3)设点A关于x轴的对称点为
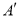 ,连接
,连接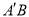 ,在点P运动的过程中,∠
,在点P运动的过程中,∠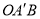 的度数是否会发生变化,若不变,请求出∠
的度数是否会发生变化,若不变,请求出∠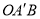 的度数,若改变,请说明理由。
的度数,若改变,请说明理由。
相关试题

