【题目】在平面直角坐标系xOy中,点A的坐标为(2,1),正比例函数y=kx的图象与线段OA的夹角是45°,求这个正比例函数的表达式为___________.
参考答案:
【答案】![]() 或
或![]()
【解析】由直线y=kx与线段OA的夹角是45°可知,本题有两种情况:一种是直线y=kx在线段OA的上方(即直线y=kx的图象经过第一、三象限);另一种是直线y=kx在线段OA的下方(直线y=kx的图象经过第二、四象限).再通过以直线y=kx与OA构造等腰直角三角形即可进行求解.
解:有两种情况:
①当直线y=kx在线段OA的上方时(即直线y=kx的图象经过第一、三象限),
如图所示,过点A作AB⊥OA,交直线y=kx于点B,过点A作平行于y轴的直线交x轴于点C,过点B作BD⊥AC,垂足为D.
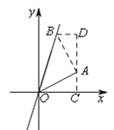
∵AB⊥OA
∴∠OAB=90°
∵∠BOA=45°
∴△OAB等腰直角三角形
∴OA=OB
∵∠OAC+∠BAD =90°, ∠OAC+∠AOC =90°
∴∠BAD=∠AOC
又∵∠D=∠ACO =90°
∴△OCA≌△BAD
∴AD=OC,BD=AC
∵A(2,1),
∴OC=2,AC=1
∴AD=OC=2,BD=AC=1
∴D点坐标为(2,3) ∴B点坐标为(1,3)
∴此时正比例函数表达式为:y=3x
②当直线y=kx在线段OA的下方时(即直线y=kx的图象经过第二、四象限):
过点A作AB⊥OA,交直线y=kx于点B,过点A作平行于x轴的直线交y轴于点C,过点B作BD⊥AC .

则由①可知:
∴△OCA≌△BAD
∴AD=OC,BD=AC
∵A(2,1),
∴OC=1,AC=2
∴AD=OC=1,BD=AC=2
∴D点坐标为(3,1)
∴B点坐标为(3,﹣1)
∴此时正比例函数表达式为:y=![]() x
x
∴正比例函数表达式为:![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(2,4)关于原点对称点的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种病毒变异后的直径约为0.000 000 56米,将这个数用科学记数法表示为_____米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AC、BD交于点M,过B、D两点分别作AC的垂线段BF、DE,AB=CD.
(1)若∠A=∠C,求证FM=EM;
(2)若FM=EM,则∠A=∠C.是真命题吗?(直接判断,不必证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果(a+b)2﹣(a﹣b)2=4,则一定成立的是( )
A. a是b的相反数B. a是﹣b的相反数
C. a是b的倒数D. a是﹣b的倒数
-
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发型了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQO使得∠O=90°,点Q在在直角坐标系y轴正半轴上,点P在x轴正半轴上,点O与原点重合,∠OQP=60°,点H在边QO上,点D、E在边PO上,点G、F在边PQ上,那么点P坐标为___________.
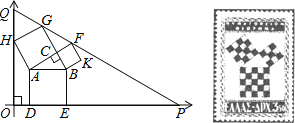
-
科目: 来源: 题型:
查看答案和解析>>【题目】某店每天卖出300只粽子,卖出一只粽子的得润为1元。经调查发现,零售单价每降0.1元,每天可多卖出100只粽子。为了使每天获得的利润更多,该店决定把零售单价下降m(0<m<1)元.
(1)零售单价降价后,该店每天可售出 只粽子,利润为 元。
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元,且卖出的粽子更多?
相关试题

