[题目]下列方程:①,②,③,④,⑤,⑥.其中是二元一次方程的是( )A.①B.①④C.①③D.①②④⑥ 题目和参考答案 ——青夏教育精英家教网—

【题目】下列方程：①；②；③；④；⑤；⑥，其中是二元一次方程的是（）

A.①B.①④C.①③D.①②④⑥

【答案】B

【解析】

根据二元一次方程满足的条件：含有2个未知数，未知数的项的次数是1的整式方程来进行解答即可；

解：①该方程中含有两个未知数，并且未知数的项的次数都是1的整式方程，所以它是二元一次方程；

②该方程是分式方程，所以它不是二元一次方程；

③该方程中的未知数的次数是2，所以它不是二元一次方程；

④由原方程得到2x+2y=0，该方程中含有两个未知数，并且未知数的项的次数都是1的整式方程，所以它是二元一次方程；

⑤该方程中含有一个未知数，所以它不是二元一次方程；

⑥该方程是分式方程，所以它不是二元一次方程；

综上所述，属于二元一次方程的是：①，④；

故答案是：B.

相关试题

科目： 来源： 题型：

【题目】下列条件中，不能判断△ABC是直角三角形的是（　　）
A. a：b：c＝3：4：5 B. ∠A：∠B：∠C＝3：4：5
C. ∠A+∠B＝∠C D. a：b：c＝1：2：
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，∠AOB=90°，OA=90cm，OB=30cm，一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球．如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是多少?
查看答案和解析>>
科目： 来源： 题型：

【题目】在一条东西走向河的一侧有一村庄C，河边原有两个取水点A，B，其中AB＝AC，由于某种原因，由C到A的路现在已经不通，某村为方便村民取水决定在河边新建一个取水点H（A、H、B在一条直线上），并新修一条路CH，测得CB＝3千米，CH＝2.4千米，HB＝1.8千米．
（1）问CH是否为从村庄C到河边的最近路？（即问：CH与AB是否垂直？）请通过计算加以说明；
（2）求原来的路线AC的长．
查看答案和解析>>

科目： 来源： 题型：

【题目】在“元旦”期间，平价商场对该商场商品进行如下的优惠促销活动：

按上述优惠条件，若小华一次性购买售价为 80 元/件的商品 n 件时，实际付款 504 元，则 n=_____.

查看答案和解析>>

科目： 来源： 题型：

【题目】阅读小强同学数学作业本上的截图内容并完成任务：
解方程组
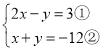
解：由①，得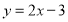，③ 第一步
把③代入①，得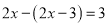．第二步
整理得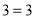，．第三步
因为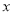可以取任意实数，所以原方程组有无数个解第四步
任务：（1）这种解方程组的方法称为；
（2）利用此方法解方程组的过程中所体现的数学思想是；（请你填写正确选项）
A．转化思想 B．函数思想 C．数形结合思想 D．公理化思想
（3）小强的解法正确吗？ (填正确或不正确)，如果不正确，请指出错在第步，请选择恰当的解方程组的方法解该方程组．
查看答案和解析>>
科目： 来源： 题型：

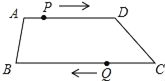
【题目】如图，在四边形ABCD中，AD∥BC，AD＝12cm，BC＝15cm，点P自点A向D以1cm/s的速度运动，到D点即停止．点Q自点C向B以2cm/s的速度运动，到B点即停止，点P，Q同时出发，设运动时间为t（s）．
（1）用含t的代数式表示：
AP＝　　；DP＝　　；BQ＝　　；CQ＝　　．
（2）当t为何值时，四边形APQB是平行四边形？
（3）当t为何值时，四边形PDCQ是平行四边形？
查看答案和解析>>