【题目】某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):
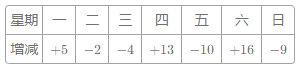
(1)产量最多的一天比产量最少的一天多生产 辆?
(2)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖20元,少生产一辆扣15元,那么该厂工人这一周的工资总额是多少元?
参考答案:
【答案】(1)26;(2)84720
【解析】
(1)用最大数减去最小数即可得到答案;
(2)根据实际生产的量乘以单价得到工资,根据超出的部分或不足的部分乘以每辆的奖金可得总奖金,根据工资加奖金得到答案.
(1)产量最多的一天比产量最少的一天多生产16-(-10)=26(辆),
故答案为:26;
(2)5-2-4+13-10+16-9=9,
该厂工人这一周的工资总额是(1400+9)![]() 60+9
60+9![]() 20=84720(元).
20=84720(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长为( )
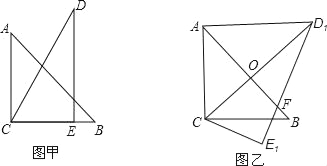
A.
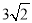 B. 5 C. 4 D.
B. 5 C. 4 D. 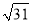
【答案】B
【解析】由旋转的性质可知,在图乙中,∠BCE1=15°,∠D1CE1=60°,AB=6,CD1=CD=7,
∴∠D1CB=60°-15°=45°,
又∵∠ACB=90°,
∴CO平分∠ACB,
又∵AC=BC,
∴CO⊥AB,且CO=AO=BO=
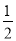 AB=3,
AB=3,∴D1O=CD1-CO=7-3=4,∠AOD1=90°,
∴在Rt△AOD1中,AD1=
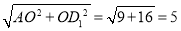 .
.故选B.
点睛:本题解题的关键是由旋转的性质证明:∠D1CB=45°,从而得到CD1平分∠ACB,结合等腰三角形的“三线合一”证得∠AOD1=90°,并求得AO=3,OD1=4;这样问题就变得很简单了.
【题型】单选题
【结束】
10【题目】我市某小区实施供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中,正确的个数有( )个.
①甲队每天挖100米;
②乙队开挖两天后,每天挖50米;
③当x=4时,甲、乙两队所挖管道长度相同;
④甲队比乙队提前2天完成任务.
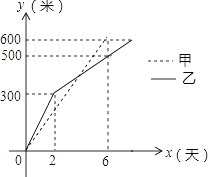
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
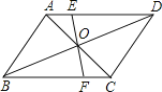
查看答案和解析>>【题目】如图所示,线段EF过平行四边形ABCD的对角线的交点O,交AD于点E,交BC于点F。已知AB=4,BC=5,EF=3,那么四边形EFCD的周长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了统计图①和图②,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为______,图①中
 的值为_____;
的值为_____;(2)本次调查获取的样本数据的众数为______,中位数为________;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?

-
科目: 来源: 题型:
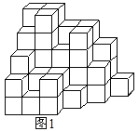
查看答案和解析>>【题目】如图1,是一个由53个大小相同的小正方体堆成的立体图形,从正面观察这个立体图形得到的平面图形如图2所示.
(1)请在图3、图4中依次画出从左面、上面观察这个立体图形得到的平面图形
(2)保持这个立体图形中最底层的小正方体不动,从其余部分中取走k个小正方体,得到一个新的立体图形.如果依次从正面、左面、上面观察新的立体图形,所得到的平面图形分别与图2、图3、图4是一样的,那么k的最大值为 .



-
科目: 来源: 题型:
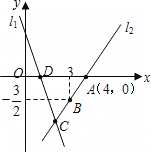
查看答案和解析>>【题目】如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2,交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在推进城乡义务教育均衡发展工作中,我市某区政府通过公开招标的方式为辖区内全部乡镇中学采购了某型号的学生用电脑和教师用笔记本电脑,其中,A乡镇中学更新学生用电脑110台和教师用笔记本电脑32台,共花费30.5万元;B乡镇中学更新学生电脑55台和教师用笔记本电脑24台,共花费17.65万元.
(1)求该型号的学生用电脑和教师用笔记本电脑单价分别是多少万元?
(2)经统计,全部乡镇中学需要购进的教师用笔记本电脑台数比购进的学生用电脑台数的
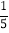 少90台,在两种电脑的总费用不超过预算438万元的情况下,至多能购进的学生用电脑和教师用笔记本电脑各多少台?
少90台,在两种电脑的总费用不超过预算438万元的情况下,至多能购进的学生用电脑和教师用笔记本电脑各多少台?
相关试题

