【题目】学之道在于悟，希望同学们在问题（1）解决过程中有所感悟，再继续探索研究问题（2）（3）．

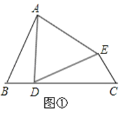
（1）如图①，D在线段BC上，∠B=∠C=∠ADE，AD=DE．求证：△ABD≌△DCE．

（2）如图②，△ABC是等腰直角三角形，∠ACB=90°，AC=BC=4，在CB的延长线上有一动点D，连接AD，以AD为直角边作等腰直角三角形ADE（∠ADE=90°，AD=DE ），连接EB并延长，与AC的延长线交于点F．当动点D在运动过程中，CF的长度是否会发生变化，如果变化，请说明理由；如果不变，请求出CF的长．

（3）如图③，射线AM与BN，MA⊥AB，NB⊥AB，点P是AB上一点， PA=1，PB=2，在射线AM与BN上分别作点C、点D，满足△CPD为等腰直角三角形．则△CPD的面积为 ．

参考答案：

【答案】（1）详见解析；（2）不变 ，CF=4；（3）面积为

【解析】

（1）利用AAS定理进行全等三角形的判定；

（2）利用等腰直角三角形的判定进行证明；

（3）分情况讨论.

（1）证明：∵ ,

,

在△ABD和△DCE中，

∴△ABD≌△DCE（AAS），

（2）不变 ，CF=4

理由为：过点E作

,

在△ACD和△DEH中，

∴△ACD≌△DHE（AAS）

∴EH=CD DH=AC

又∵AC=BC ∴DH=CB

∴DH+BD=CB+BD 即CD=BH

∴EH=BH ∴

∴∴△BCF为等腰直角三角形

∴CF=BC=4

(3)有三种情况，PC=PD、CP=CD、DC=DP，
如图所示：

图2中，当PC=PD时，由题意可证△CAP≌△PBD，∴CP= ，所以

当PC=CD时，作DE⊥AM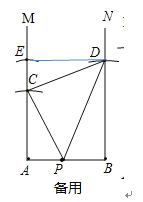

易证△EDC≌△CAP，且四边形DEAB为矩形，

∴DE=AB=3,EC=AP=1,

∴CD=

所以

当CD=PD时，

作CF⊥BN,

易证△FDC≌△CAP，且四边形DABF为矩形，

∴CF=AB=3,FD=PB=2,

∴CD=

所以

综上所述，面积为

关闭