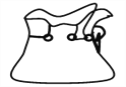
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字![]() ,另一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字
,另一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字![]() (如图).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一个人口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去,否则小亮去.
(如图).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一个人口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去,否则小亮去.
⑴.用树状图或列表法求出小颖参加比赛的概率;
⑵.你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏的规则,使游戏公平.

参考答案:
【答案】(1)小颖参加比赛的概率为![]() (2)该游戏不公平
(2)该游戏不公平
【解析】试题分析:(1)、根据题目中给出的方案画出树状图,得出所有可能出现的结果,然后找到数字之和小于4的情况,从而得出概率;(2)、根据概率不相同得出游戏不公平,修改的方案只需要满足两人的概率相同即可,答案是不唯一的.
试题解析:(1)、画树状图:
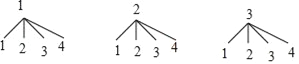
共有12种等可能性结果,其中数字之和小于4的有3种情况,
所以P(和小于4)=![]() =
=![]() ,
,
即小颖参加比赛的概率为![]() ;
;
(2)、该游戏不公平.理由如下:
因为P(和不小于4)=![]() ,所以P(和小于4)≠P(和不小于4),
,所以P(和小于4)≠P(和不小于4),
所以游戏不公平,可改为:若数字之和为偶数,则小颖去;若数字之和为奇数,则小亮去.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个长方形运动场被分隔成A,B,A,B,C共5个区,A区是边长为a m的正方形,C区是边长为c m的正方形.
(1)列式表示每个B区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果a=40,c=10,求整个长方形运动场的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现:若每箱以50元的价格出售,平均每天销售80箱,价格每提高1元,平均每天少销售2箱.
⑴.求平均每天销售量
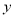 (箱)与销售价
(箱)与销售价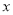 (元/箱)之间的函数关系式;
(元/箱)之间的函数关系式;⑵.求该批发商平均每天的销售利润
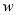 (元)与销售价
(元)与销售价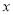 (元/箱)之间的函数关系式;
(元/箱)之间的函数关系式;⑶.当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用“”规定一种新运算:对于任意有理数a和b,规定ab=ab2+2ab+a.如:13=1×32+2×1×3+1=16
(1)求2(-1)的值;
(2)若(a+1)3=32,求a的值;
(3)若m=2x,n=(
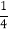 x)3(其中x为有理数),试比较m、n的大小.
x)3(其中x为有理数),试比较m、n的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D是△ABC的边AB上一点,CE∥AB,DE交AC于点F,若FA=FC.
(1)求证:四边形ADCE是平行四边形;
(2)若AE⊥EC,EF=EC=5,求四边形ADCE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是弧
 的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.⑴求证:AC=CD.
⑵若OB=2,求BH的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列方程及解的特征:
(1)x+
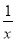 =2的解为x1=x2=1;
=2的解为x1=x2=1;(2)x+
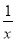 =
=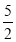 的解为x1=2,x2=
的解为x1=2,x2=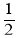 ;
;(3)x+
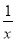 =
=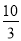 的解为x1=3,x2=
的解为x1=3,x2=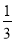 ;
; …
解答下列问题:
(1)请猜想:方程x+
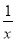 =
=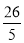 的解为______;
的解为______;(2)请猜想:关于x的方程x+
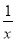 =______ 的解为x1=a,x2=
=______ 的解为x1=a,x2=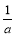 (a≠0);
(a≠0);(3)下面以解方程x+
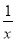 =
=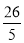 为例,验证(1)中猜想结论的正确性.
为例,验证(1)中猜想结论的正确性.(4)解方式方程

相关试题

