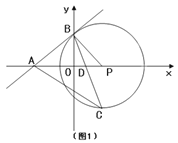
【题目】如图1,点A、B、P分别在两坐标轴上,∠APB=60°,PB=m,PA=2m,以点P为圆心、PB为半径作⊙P,作∠OBP的平分线分别交⊙P、OP于C、D,连接AC.
(1)求证:直线AB是⊙P的切线.
(2)设△ACD的面积为S,求S关于m的函数关系式.
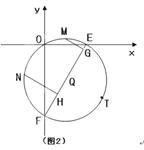
(3)如图2,当m=2时,把点C向右平移一个单位得到点T,过O、T两点作⊙Q交x轴、y轴于E、F两点,若M、N分别为两弧![]() 的中点,作MG⊥EF,NH⊥EF,垂足为G、H,试求MG+NH的值.
的中点,作MG⊥EF,NH⊥EF,垂足为G、H,试求MG+NH的值.
参考答案:
【答案】见解析
【解析】分析: (1)根据切线的判定定理证得∠ABP=90°后即可判定切线;
(2)连接PC,根据∠APB=90°-∠OBP=∠OBA,∠OBC=∠PBC,得到∠ADB=∠PBC+∠PBC=∠ABD,从而得到∠CPA=∠POB=90°,利用三角形的面积公式得到S=![]() m2;
m2;
(3)作TJ⊥x轴,TK⊥y轴,连接ET、FT,得到△ETJ≌△FTK,从而得到NH=![]() NR=
NR=![]() OF和MG=
OF和MG=![]() OE,最后求得MG+NH=
OE,最后求得MG+NH=![]() (OE+OF)=
(OE+OF)=![]() ×4=2.
×4=2.
详解:
(1)∵∠POB=90°,∠APB=60°,
∴PB=m,
∴PO=![]() PB=
PB=![]() m,OB=
m,OB=![]() m,
m,
又∵PA=2m,
∴OA=![]() m,
m,
在RT△OAB中,AB=![]() m
m
∴PA2+AB2=PA2
∴∠ABP=90°,
∵PB是⊙P的半径,
∴直线AB是⊙P的切线.
(2)连接PC,
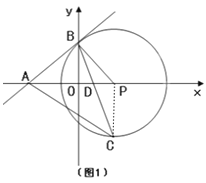
∵∠APB=90°-∠OBP=∠OBA,∠OBC=∠PBC,
∴∠ADB=∠PBC+∠PBC=∠ABD
∴AD=AB=![]() m,
m,
又∵PB=PC=m,
∴PC∥OC
∴∠CPA=∠POB=90°,
∴S△ACD=![]() AD×CP=
AD×CP=![]()
![]() m×m=
m×m=![]() m2;
m2;
(3)作TG⊥x轴,TK⊥y轴,连接ET、FT,
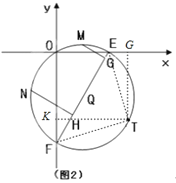
当m=2时,PO=![]() m,由(2)知∠CPA=90°,
m,由(2)知∠CPA=90°,
∴C点为 (1,-2),
∴T为(2,-2,)TG=TK=2,
∴点T在∠EOF的平分线上,∴![]()
∴TE=TF,
∴△ETG≌△FTK,
∴EF=EG,
∴OE+OF=OG-EG+OK+FK=OG+OK=4
延长NH交⊙Q于R,连接QN,QR,∵∠EOF=90°,
∴EF为⊙Q的直径,∴![]()
![]()
![]()
∴NR=OF
∴NH=![]() NR=
NR=![]() OF
OF
同理MG=![]() OE
OE
∴MG+NH=![]() (OE+OF)=
(OE+OF)=![]() ×4=2
×4=2
点睛: 本题考查了圆的综合知识,难度较大,一般为中考题的压轴题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个,2个甲种部件和3个乙种部件配成一套,问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套?并求出加工了多少套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】现在,某商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果红旗商场还能盈利25%,这台冰箱的进价是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
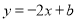 分别于
分别于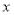 轴、
轴、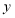 轴交于A、B两点,与直线
轴交于A、B两点,与直线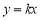 交于点C(2,4),平行于
交于点C(2,4),平行于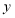 轴的直线
轴的直线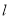 从原点
从原点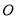 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿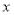 轴向右平移,直线
轴向右平移,直线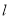 分别交直线AB、直线OC于点D、E,以DE为边向左侧作正方形DEFG,当直线
分别交直线AB、直线OC于点D、E,以DE为边向左侧作正方形DEFG,当直线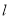 经过点A时停止运动,设直线
经过点A时停止运动,设直线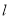 的运动时间为
的运动时间为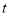 (秒).
(秒).(1)
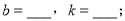
(2)设线段DE的长度为
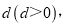 求
求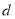 与
与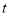 之间的函数关系式;
之间的函数关系式;(3)当正方形DEFG的边GF落在
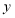 轴上,求出
轴上,求出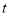 的值;
的值;(4)当
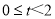 时,若正方形DEFG和△OCB重叠部分面积为4,则
时,若正方形DEFG和△OCB重叠部分面积为4,则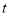 的值为________.
的值为________.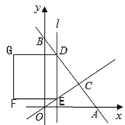
-
科目: 来源: 题型:
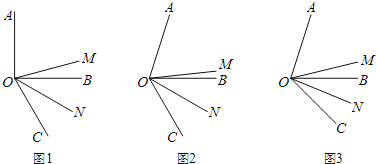
查看答案和解析>>【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的边OA,OC分别在
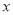 轴、
轴、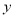 轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应),若AB=1,反比例函数
轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应),若AB=1,反比例函数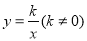 的图象恰好经过点 A′,B,则
的图象恰好经过点 A′,B,则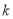 的值为_________.
的值为_________.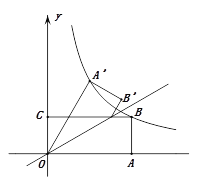
-
科目: 来源: 题型:
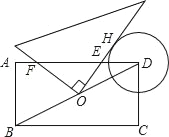
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则tan∠EFO的值为_____.
相关试题

