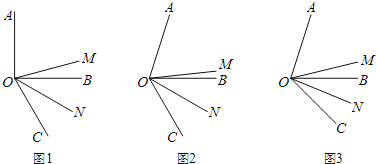
【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.
参考答案:
【答案】(1)45°;(2)∠MON=![]() α.(3)∠MON=
α.(3)∠MON=![]() α
α
【解析】
试题分析:(1)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC﹣∠NOC求出即可;
(2)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC﹣∠NOC求出即可;
(3)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC﹣∠NOC求出即可.
解:(1)如图1,∵∠AOB=90°,∠BOC=60°,
∴∠AOC=90°+60°=150°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=![]() ∠AOC=75°,∠NOC=
∠AOC=75°,∠NOC=![]() ∠BOC=30°
∠BOC=30°
∴∠MON=∠MOC﹣∠NOC=45°.
(2)如图2,∠MON=![]() α,
α,
理由是:∵∠AOB=α,∠BOC=60°,
∴∠AOC=α+60°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=![]() ∠AOC=
∠AOC=![]() α+30°,∠NOC=
α+30°,∠NOC=![]() ∠BOC=30°
∠BOC=30°
∴∠MON=∠MOC﹣∠NOC=(![]() α+30°)﹣30°=
α+30°)﹣30°=![]() α.
α.
(3)如图3,∠MON=![]() α,与β的大小无关.
α,与β的大小无关.
理由:∵∠AOB=α,∠BOC=β,
∴∠AOC=α+β.
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠MOC=![]() ∠AOC=
∠AOC=![]() (α+β),
(α+β),
∠NOC=![]() ∠BOC=
∠BOC=![]() β,
β,
∴∠AON=∠AOC﹣∠NOC=α+β﹣![]() β=α+
β=α+![]() β.
β.
∴∠MON=∠MOC﹣∠NOC
=(α+β)﹣
![]() β=
β=![]() α
α
即∠MON=![]() α.
α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现在,某商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果红旗商场还能盈利25%,这台冰箱的进价是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
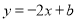 分别于
分别于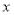 轴、
轴、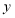 轴交于A、B两点,与直线
轴交于A、B两点,与直线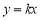 交于点C(2,4),平行于
交于点C(2,4),平行于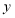 轴的直线
轴的直线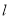 从原点
从原点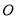 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿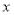 轴向右平移,直线
轴向右平移,直线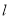 分别交直线AB、直线OC于点D、E,以DE为边向左侧作正方形DEFG,当直线
分别交直线AB、直线OC于点D、E,以DE为边向左侧作正方形DEFG,当直线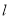 经过点A时停止运动,设直线
经过点A时停止运动,设直线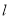 的运动时间为
的运动时间为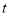 (秒).
(秒).(1)
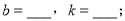
(2)设线段DE的长度为
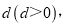 求
求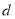 与
与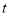 之间的函数关系式;
之间的函数关系式;(3)当正方形DEFG的边GF落在
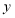 轴上,求出
轴上,求出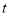 的值;
的值;(4)当
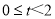 时,若正方形DEFG和△OCB重叠部分面积为4,则
时,若正方形DEFG和△OCB重叠部分面积为4,则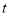 的值为________.
的值为________.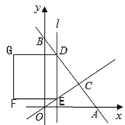
-
科目: 来源: 题型:
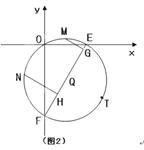
查看答案和解析>>【题目】如图1,点A、B、P分别在两坐标轴上,∠APB=60°,PB=m,PA=2m,以点P为圆心、PB为半径作⊙P,作∠OBP的平分线分别交⊙P、OP于C、D,连接AC.
(1)求证:直线AB是⊙P的切线.
(2)设△ACD的面积为S,求S关于m的函数关系式.
(3)如图2,当m=2时,把点C向右平移一个单位得到点T,过O、T两点作⊙Q交x轴、y轴于E、F两点,若M、N分别为两弧
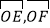 的中点,作MG⊥EF,NH⊥EF,垂足为G、H,试求MG+NH的值.
的中点,作MG⊥EF,NH⊥EF,垂足为G、H,试求MG+NH的值.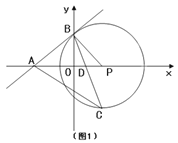
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的边OA,OC分别在
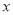 轴、
轴、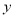 轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应),若AB=1,反比例函数
轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应),若AB=1,反比例函数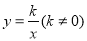 的图象恰好经过点 A′,B,则
的图象恰好经过点 A′,B,则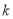 的值为_________.
的值为_________.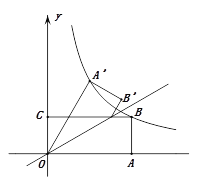
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则tan∠EFO的值为_____.
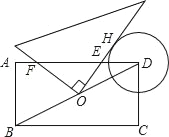
-
科目: 来源: 题型:
查看答案和解析>>【题目】有如下说法:①直线是一个平角;②如果线段AB=BC,则B是线段AC的中点;③射线AB与射线BA表示同一射线;④用一个扩大2倍的放大镜去看一个角,这个角扩大2倍;⑤两点之间,直线最短;⑥120.5°=120°30′,其中正确的有( )
A.1个B.2个C.3个D.4个
相关试题

