【题目】问题引入:
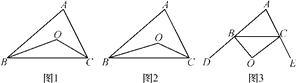
(1)如图1,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);
如图2,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,则∠BOC= (用α表示);
∠ACB,∠A=α,则∠BOC= (用α表示);
拓展研究:
(2)如图3,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() .
.
【解析】试题分析:(1)点O是∠ABC和∠ACB平分线的交点,所以∠BOC=180°-∠OBC-∠OCB=180°-![]() (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°-![]() (180°-α)=
(180°-α)=![]() ;同理得图2:∠BOC=
;同理得图2:∠BOC=![]() ;(2)见解析(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,∠A=α,则∠BOC=180°-∠OBC-∠OCB=180°-
;(2)见解析(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,∠A=α,则∠BOC=180°-∠OBC-∠OCB=180°-![]() (∠DBC+∠ECB)=180°-
(∠DBC+∠ECB)=180°-![]() (180°-∠ABC+180°-∠ACB)=180°-
(180°-∠ABC+180°-∠ACB)=180°-![]() (180°+180°-∠ABC-∠ACB)= 180°-
(180°+180°-∠ABC-∠ACB)= 180°-![]() (180°+
(180°+![]() )=
)=![]() .
.
试题解析:
(1)![]() ,
,![]() ;
;
(2)![]() ,
,
理由:∵∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,
∠ECB,∠A=α,
∴∠BOC=180°-![]() (∠DBC+∠ECB)
(∠DBC+∠ECB)
=180°-![]() [360°-(∠ABC+∠ACB)]
[360°-(∠ABC+∠ACB)]
=180°-![]() [360°-(180°-∠A)]
[360°-(180°-∠A)]
=180°-![]() (180°+∠α)
(180°+∠α)
=180°-60°-![]() ∠α
∠α
=120°-![]() ∠α.;
∠α.;
(3)![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,CE平分∠ACB交AB于点E,CE=BC.
(1)求∠A的度数;
(2)能否在AC边上找一点D,并连接ED,使△AED≌△CEB?若能,请作出你找的点,并证明;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图所示,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F.H是BC边上的中点,连接DH与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE=
 BF;
BF;(3)请你根据该题的条件并结合图形,自己提出一个问题,并解答或证明你提出的问题.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某剧院舞台上的照明灯P射出的光线成“锥体”,其“锥体”面图的“锥角”是60°.已知舞台ABCD是边长为6m的正方形.要使灯光能照射到整个舞台,则灯P的悬挂高度是( )

A.3 m
m
B.3 m
m
C.4 m
m
D. m
m -
科目: 来源: 题型:
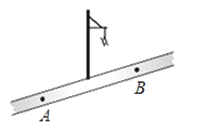
查看答案和解析>>【题目】如图,小红晚上在一条笔直的小路上由A处径直走到B处,小路的正中间有一盏路灯,那么小红在灯光照射下的影长l与她行走的路程s之间的变化关系用图象刻画出来大致是( )
A.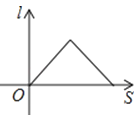
B.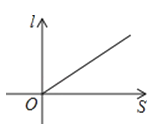
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直角坐标平面内,一点光源位于A(0,5)处,线段CD⊥x轴,D为垂足,C(3,1),则CD在x轴上的影长为 ,点C的影子的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一间黑屋里用一白炽灯照射一个球,
(1)球在地面上的阴影是什么形状?
(2)当把白炽灯向上移时,阴影的大小会怎样变化?
(3)若白炽灯到球心距离为1米,到地面的距离是3米,球的半径是0.2米,求球在地面上阴影的面积是多少?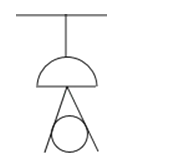
相关试题

