【题目】某校九年级学生开展踢毽子比赛活动,每班派5名同学参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
1号 | 2号 | 3号 | 4号 | 5号 | 总分 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
统计发现两班总分相等,此时有同学建议,可以通过考查数据中的其他信息作为参考,请你解答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)估计两班比赛数据的方差哪一个小?
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班?简述理由.
参考答案:
【答案】(1) 甲:60%;乙:40%;(2)甲:100,乙:97;
(3)甲的方差小;(4)甲班,理由见解析.
【解析】试题分析:
(1)甲班优秀学生数为3,乙班优秀学生数为2,优秀率=优秀学生数÷学生总数×100%;(2)根据中位数是按次序排列后的第3个数即可;(3)根据方差的计算公式计算即可得到两班比赛数据的方差;(4)根椐以上三条信息,综合分析即可即可得结论.
试题解析:
(1)甲班的优秀率是![]() ×100%=60%;乙班的优秀率是
×100%=60%;乙班的优秀率是![]() ×100%=40%;
×100%=40%;
(2)甲班5名学生比赛成绩的中位数为100(个);乙班5名学生成绩的中位数为97(个);
(3) ![]() 甲=
甲=![]() ×500=100(个),
×500=100(个), ![]() 乙=
乙=![]() ×500=100(个);
×500=100(个);
s甲2=![]() [(100-100)2+(98-100)2+(110-100)2+(89-100)2+(103-100)2]=46.8,
[(100-100)2+(98-100)2+(110-100)2+(89-100)2+(103-100)2]=46.8,
s乙2=![]() [(89-100)2+(100-100)2+(95-100)2+(119-100)2+(97-100)2]=103.2,
[(89-100)2+(100-100)2+(95-100)2+(119-100)2+(97-100)2]=103.2,
∴甲班的方差小;
(4)因为甲班5人比赛成绩的优秀率比乙班高、中位数比乙班大、方差比乙班小,应该把冠军奖状发给甲班.
-
科目: 来源: 题型:
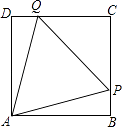
查看答案和解析>>【题目】如图,在边长为10的正方形ABCD中,△PAQ是正三角形,求PB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长城公司为希望小学捐赠甲、乙两种品牌的体育器材,甲品牌有A、B、C三种型号,乙品牌有D、E两种型号,现要从甲、乙两种品牌的器材中各选购一种型号进行捐赠.
(1)写出所有的选购方案(用列表法或树状图);
(2)如果在上述选购方案中,每种方案被选中的可能性相同,那么A型器材被选中的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】从甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
甲:79,86,82,85,83;乙:88,79,90,81,72.
请回答下列问题:
(1)甲成绩的平均数是______,乙成绩的平均数是______;
(2)经计算知
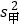 =6,
=6,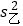 =42,你认为选谁参加比赛更合适,说明理由.
=42,你认为选谁参加比赛更合适,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小红的奶奶开了一个金键牛奶销售店,主要经营“金键学生奶”、“金键酸牛奶”、“金键原味奶”,由于经营不善,经常导致牛奶滞销(没卖完)或脱销(量不够),为此细心的小红结合所学知识帮奶奶统计了一个星期牛奶的销售情况,并绘制成下表:
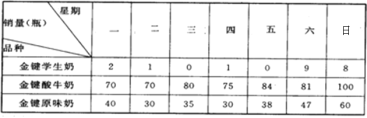
(1)计算各品种牛奶的日平均销售量,并说明哪种牛奶销量最高;
(2)计算各品种牛奶的方差(保留两位小数),并比较哪种牛奶销量最稳定;
(3)假如你是小红,会给奶奶哪些建议?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF. 求证:四边形BCFE是菱形.

相关试题

