【题目】如图,在边长为10的正方形ABCD中,△PAQ是正三角形,求PB的长. 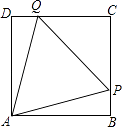
参考答案:
【答案】解:设PB=x, ∴PC=10﹣x,
由题意可知:AD=AB,AQ=AP
在Rt△AQD与Rt△APB中,![]()
∴Rt△AQD≌Rt△APB(HL)
∴DQ=PB=x,
∴CQ=10﹣x,
在Rt△APB中,AP2=100+x2 ,
在Rt△CQP中,AP2=CQ2+PC2 ,
∴100+x2=2(10﹣x)2
化简:x2﹣40x+100=0,
解得:x=20±10 ![]() ,
,
∵x<10,
∴PB=x=20﹣10 ![]()
【解析】设PB=x,根据正方形以及等边三角形的性质求出PQ与PC的表达式,然后利用勾股定理列出方程求出x的值.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF=cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次男子马拉松长跑比赛中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据:140 146 143 175 125 164 134 155 152 168 162 148
(1)计算该样本数据的中位数和平均数;
(2)如果一名选手的成绩是147分钟,请你依据样本数据的中位数,推断他的成绩如何?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)2x2﹣4x﹣3=0(配方法)
(2)x(x+2)=2+x. -
科目: 来源: 题型:
查看答案和解析>>【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长城公司为希望小学捐赠甲、乙两种品牌的体育器材,甲品牌有A、B、C三种型号,乙品牌有D、E两种型号,现要从甲、乙两种品牌的器材中各选购一种型号进行捐赠.
(1)写出所有的选购方案(用列表法或树状图);
(2)如果在上述选购方案中,每种方案被选中的可能性相同,那么A型器材被选中的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级学生开展踢毽子比赛活动,每班派5名同学参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
1号
2号
3号
4号
5号
总分
甲班
100
98
110
89
103
500
乙班
89
100
95
119
97
500
统计发现两班总分相等,此时有同学建议,可以通过考查数据中的其他信息作为参考,请你解答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)估计两班比赛数据的方差哪一个小?
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班?简述理由.
相关试题

