【题目】如图,锐角△ABC的两条高BD与CE相交于点O,且OB=OC,连接AO.

(1)求证:∠ABC=∠ACB;
(2)求证:AO垂直平分线段BC.
参考答案:
【答案】(1)见解析;(2)见解析
【解析】
(1)由OB=OC,即可求得∠OBC=∠OCB,又由,锐角△ABC的两条高BD、CE相交于点O,根据三角形的内角和等于180°,即可证得结论.
(2)首先连接AO并延长交BC于F,通过证△AOB≌△AOC(SSS),得到∠BAF=∠CAF,再利用等腰三角形的性质可得结论.
(1)证明:∵OB=OC,
∴∠OBC=∠OCB,
∵锐角△ABC的两条高BD、CE相交于点O,
∴∠BEC=∠CDB=90°,
∵∠BEC+∠BCE+∠ABC=∠CDB+∠DBC+∠ACB=180°,
∴180°﹣∠BEC﹣∠BCE=180°﹣∠CDB﹣∠CBD,
∴∠ABC=∠ACB,
(2)证明:AO垂直平分线段BC.
理由:连接AO并延长交BC于F,
∵∠ABC=∠ACB,
∴AB=AC
在△AOB和△AOC中,
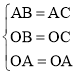 ,
,
∴△AOB≌△AOC(SSS).
∴∠BAF=∠CAF,
∵AB=AC,
∴AO垂直平分线段BC.
-
科目: 来源: 题型:
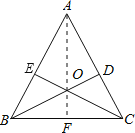
查看答案和解析>>【题目】李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米.要围成的菜园是如图所示的矩形ABCD.设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是( )

A. y=-2x+24(0<x<12) B. y=-
 x+12(0<x<24)
x+12(0<x<24)C. y=2x-24(0<x<12) D. y=
 x-12(0<x<24)
x-12(0<x<24) -
科目: 来源: 题型:
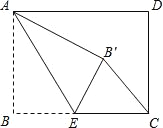
查看答案和解析>>【题目】矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )
A. 3 B.
 C. 2或3 D. 3或
C. 2或3 D. 3或
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标是(﹣2,3),点B的坐标是(1,﹣1),连接AB,点C是坐标轴上任意一点,则使△ABC为等腰三角形的点C共有_____个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名队员参加射击训练,每人射击10次,成绩分别如下:

根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)a=_____;b=_____;c=_____;
(2)填空:(填“甲”或“乙”).
①从平均数和中位数的角度来比较,成绩较好的是_____;
②从平均数和众数的角度来比较,成绩较好的是_____;
③成绩相对较稳定的是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=-
 x+b的图象与x轴,y轴分别交于点A,B,与一次函数y=
x+b的图象与x轴,y轴分别交于点A,B,与一次函数y= x的图象交于点M,点M的横坐标为
x的图象交于点M,点M的横坐标为 ,在x轴上有一点P(a,0),过点P作x轴的垂线,分别交一次函数y=-
,在x轴上有一点P(a,0),过点P作x轴的垂线,分别交一次函数y=- x+b和一次函数y=
x+b和一次函数y= x的图象于点C,D.
x的图象于点C,D.
(1)点M的纵坐标是 ;b的值是 ;
(2)求线段AB的长;
(3)当CD=AB时,请直接写出a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一笔直的公路连接M,N两地,甲车从M地驶往N地,速度为60km/h,乙车从M地驶往N地,速度为40km/h,丙车从N地驶往M地,速度为80km/h,三辆车同时出发,先到目的地的车停止不动.途中甲车发生故障,于是停车修理了2.5h,修好后立即按原速驶往N地.设甲车行驶的时间为t(h),甲、丙两车之间的距离为S1(km).甲、乙两车离M地的距离为S2(km),S1与t之间的关系如图1所示,S2与t之间的关系如图2所示.根据题中的信息回答下列问题:

(1)①图1中点C的实际意义是 ;
②点B的横坐标是 ;点E的横坐标是 ;点Q的坐标是 ;
(2)请求出图2中线段QR所表示的S2与t之间的关系式;
(3)当甲、乙两车距70km时,请直接写出t的值.
相关试题

