搜索
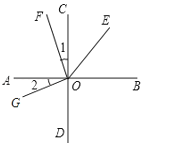
【题目】已知：如图， AB⊥CD于点O，∠1=∠2，OE平分∠BOF，∠EOB=55°，求∠GOF和∠DOG的度数．
参考答案：
【答案】90°；70°
【解析】
先由垂直的定义可得∠1+∠AOF=90°，再由∠1=∠2，即可求得∠GOF=90°，根据角平分线的定义可得∠BOF=2∠EOB=110°，根据平角定义可求得∠AOF=70°，继而可得∠1 =20°，再根据平角定义即可求得∠DOG的度数.
∵AB⊥CD，
∴∠AOC=90°，即∠1+∠AOF=90°，
又∵∠1=∠2，
∴∠2+∠AOF=90°，
即∠GOF=90°，
∵OE平分∠BOF，∠EOB=55°，
∴∠BOF=2∠EOB=110°，
∴∠AOF=180°-∠BOF=70°，
∴∠1=∠AOC-∠AOF=20°，
∴∠DOG=180°-∠1-∠GOF=70°.
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）已知a+b＝﹣
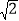，求代数式（a﹣1）2+b（2a+b）+2a的值．（2）已知a，b，c是三角形的三边，且a2+b2+c2﹣ab﹣bc﹣ac＝0．求证：此三角形是等边三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某地管辖A，B，C，D四个镇，其中C，A，D三个镇在一条直线上，相互两镇之间的公路里程如图所示，由于大山阻隔，原来从A，C两镇去D镇都需绕到B镇前往．为了发展经济，缩短A，C两镇到D镇的路程，现决定开凿隧道修通A，C两镇直达D镇的公路AD.公路修通后从A镇去D镇的路程比原来缩短了多少千米？(参考数据：
＝32，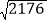
≈46.65)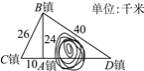
-
科目： 来源： 题型：
查看答案和解析>>【题目】以下是两张不同类型火车的车票：（“D×××次”表示动车，“G×××次”表示高铁）：
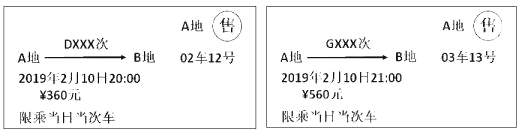
（1）根据车票中的信息填空：两车行驶方向 ，出发时刻 （填“相同”或“不同”）；
（2）已知该动车和高铁的平均速度分别为200km/h，300km/h，如果两车均按车票信息准时出发，且同时到达终点，求A，B两地之间的距离；
（3）在（2）的条件下，请求出在什么时刻两车相距100km？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠A=60°，点D是BC边的中点，DE⊥BC，∠ABC的角平分线BF交DE于△ABC内一点P，连接PC．
（1）若∠ACP=24°，求∠ABP的度数；
（2）若∠ACP=m°，∠ABP=n°，请直接写出m，n满足的关系式： ． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知点O为直线AB上一点，将直角三角板MON的直角顶点放在点O处，并在∠MON内部作射线OC．
（1）如图1，三角板的一边ON与射线OB重合，且∠AOC＝150°．若以点O为观察中心，射线OM表示正北方向，求射线OC表示的方向；
（2）如图2，将三角板放置到如图位置，使OC恰好平分∠MOB，且∠BON＝2∠NOC，求∠AOM的度数；
（3）若仍将三角板按照如图2的方式放置，仅满足OC平分∠MOB，试猜想∠AOM与∠NOC之间的数量关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校组织甲、乙两队开展“保护生态环境知识竞赛”，满分为10分，得分均为整数，规定得分达到6分及以上为合格，达到9分及以上为优秀，如图是甲、乙两队学生这次竞赛成绩分布条形统计图．
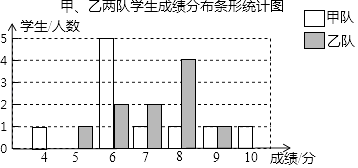
根据以上信息，请解答下面的问题：
（1）在下面甲、乙两队的成绩统计表中，a= ， b=c= ．平均分
中位数
众数
方差
合格率
优秀率
甲队
a
6
c
2.76
90%
20%
乙队
7.2
b
8
1.36
80%
10%
（2）小华同学说：“我在这次比赛中得到了7分，这在我所在的小队成绩中属于中等偏上的位置！”观察（1）中的表格，小华是队的学生；（填“甲”或“乙”）
（3）甲队同学认为：甲队的合格率、优秀率均高于乙队，所以甲队的成绩好于乙队．但乙队同学不同意甲队同学的说法，认为乙队的成绩要好于甲队．请你写出两条支持乙队同学观点的理由．
（4）学校要从从甲、乙两队获得优秀的学生中，选取两名同学参加市级比赛，则恰好同时选中的两人均为甲队学生的概率为 ．
相关试题
