【题目】在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;
(2)如果点P的坐标是(﹣a,0),其中a>0,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.

参考答案:
【答案】(1)A2(4,0),B2(5,0),C2(5,2)
(2)6.
【解析】试题分析:(1)根据关于y轴对称点的坐标特点是横坐标互为相反数,纵坐标相同可以得到△A1B1C1各点坐标,又关于直线l的对称图形点的坐标特点是纵坐标相同,横坐标之和等于3的二倍,由此求出△A2B2C1的三个顶点的坐标;
(2)P与P1关于y轴对称,利用关于y轴对称点的特点:纵坐标不变,横坐标变为相反数,求出P1的坐标,再由直线l的方程为直线x=3,利用对称的性质求出P2的坐标,即可PP2的长.
试题解析:(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2);
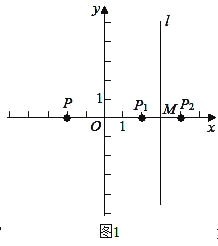
(2)如图1,当0<a≤3时,∵P与P1关于y轴对称,P(-a,0),
∴P1(a,0),
又∵P1与P2关于l:直线x=3对称,
设P2(x,0),可得:![]() =3,即x=6-a,
=3,即x=6-a,
∴P2(6-a,0),
则PP2=6-a-(-a)=6-a+a=6.
如图2,当a>3时,
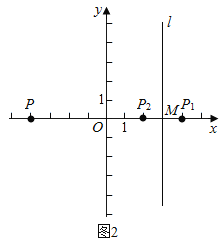
∵P与P1关于y轴对称,P(-a,0),
∴P1(a,0),
又∵P1与P2关于l:直线x=3对称,
设P2(x,0),可得:![]() =3,即x=6-a,
=3,即x=6-a,
∴P2(6-a,0),
则PP2=6-a-(-a)=6-a+a=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判断正确的是( )
A. 两边和一角对应相等的两个三角形全等 B. 一边及一锐角相等的两个直角三角形全等
C. 顶角和底边分别相等的两个等腰三角形全等 D. 三个内角对应相等的两个三角形全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】在知识抢答中,如果用+10表示得10分,那么扣30分表示为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个直角三角形中,它的一个锐角的外角为135°,则这个三角形_____对称轴.(填“有”或“没有”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,将坐标是(3,0),(3,2),(0,3),(3,5),(3,2),(6,3),(6,2),(3,0),(6,0)的点用线段依次连接起来形成一个图案.
(1)作出原图案关于x轴对称的图案.两图案中的对应点的坐标有怎样的关系?
(2)作出原图案关于y轴对称的图案.两图案中的对应点的坐标有怎样的关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,正方形ABCD的顶点坐标分别为 A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点 P(0,2).作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称轴P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5,作点P5关于点B的对称点P6,…,按此操作下去,则点P2016的坐标为( )
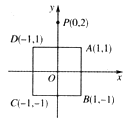
A. (0,2) B. (2,0) C. (0,-2) D. (-2,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 (x+1)(x﹣3)与x轴交于A、B两点,与y轴交于点C,点D为该抛物线的对称轴上一点,当点D到直线BC和到x轴的距离相等时,则点D的坐标为 .
(x+1)(x﹣3)与x轴交于A、B两点,与y轴交于点C,点D为该抛物线的对称轴上一点,当点D到直线BC和到x轴的距离相等时,则点D的坐标为 .
相关试题

