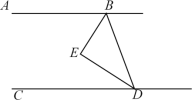
【题目】如图,AB∥CD,BE平分∠ABD,DE平分∠BDC。
(1)求证:BE⊥DE;
(2)H是直线CD上一动点(不与D重合),HI平分∠HBD交CD于点I。请你画出图形,并猜想∠EBI与∠BHD的数量关系,且说明理由。
参考答案:
【答案】(1)见解析;(2)当H在点D的左侧时,∠BHD=2∠EBI;当H在点D的右侧时,∠BHD=180°-2∠EBI;理由见解析
【解析】
(1)根据平行线的性质以及角平分线的定义,即可得到BE⊥DE;
(2)根据角平分线的定义可得∠ABD=2∠EBD;∠HBD=2∠DBI,然后分点H在点D的左边和右边两种情况,表示出∠ABH和∠BHD,从而得解
(1)证明:过点E作EF∥AB
∴∠ABE=∠BEF
又∵AB∥CD
∴∠ABD+∠BDC=180°,EF∥CD,
∴∠FED=∠CDE
∵BE平分∠ABD,DE平分∠BDC,
∴∠ABE=![]() ∠ADB,∠CDE=
∠ADB,∠CDE=![]() ∠BDC,
∠BDC,
∴∠ABE+∠CDE=![]() ×180°=90°
×180°=90°
∴∠BEF+∠FED=90°,即∠BED=90°
∴BE⊥DE

(2)①当H在点D的左侧时,∠BHD=2∠EBI;
证明:∵AB∥CD
∴∠ABH=∠BHD;
∵BE平分∠ABD,BI平分∠HBD,
∴∠ABD=2∠EBD;∠HBD=2∠DBI;
∠ABH=∠ABD-∠HBD=2(∠EBD-∠DBI)=2∠EBI;
∴∠BHD=2∠EBI;
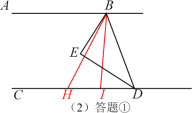
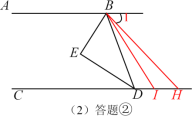
②当H在点D的右侧时,∠BHD=180°-2∠EBI;
证明:∵AB∥CD
∴∠BHD=∠1;
又∵∠1+∠ABH=180°;
∴∠1+∠ABD+∠DBH=180°,
∵BE平分∠ABD,BI平分∠HBD,
∴∠ABD=2∠EBD;∠HBD=2∠DBI;
∴∠1+2∠EBD+2∠DBI=180°,
∴∠1=180°-2(∠EBD+∠DBI) =180°-2∠EBI,
即∠BHD=180°-2∠EBI。
-
科目: 来源: 题型:
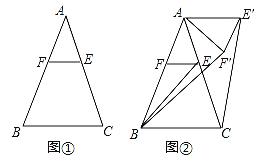
查看答案和解析>>【题目】已知,△ABC中,AB=AC,点E是边AC上一点,过点E作EF∥BC交AB于点F
(1)如图①,求证:AE=AF;
(2)如图②,将△AEF绕点A逆时针旋转α(0°<α<144°)得到△AE′F′.连接CE′BF′.
①若BF′=6,求CE′的长;
②若∠EBC=∠BAC=36°,在图②的旋转过程中,当CE′∥AB时,直接写出旋转角α的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为更好地践行社会主义核心价值观,让同学们珍惜粮食,学会感恩,校学生会积极倡导“光盘小行动”,某天午餐后学生会干部随机调查了部分同学就餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
(1)这次被调查的同学共有 名;
(2)补全条形统计图;
(3)计算在扇形统计图中剩大量饭菜所对应扇形圆心的度数;
(4)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人用一餐,据此估算,全校
 名学生一餐浪费的食物可供多少人食用一餐?
名学生一餐浪费的食物可供多少人食用一餐?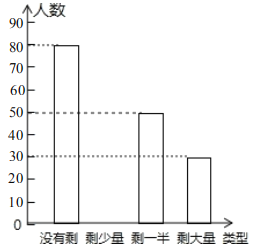

-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, 分别是
分别是 的中点,若等腰
的中点,若等腰 绕点
绕点 逆时针旋转,得到等腰
逆时针旋转,得到等腰 ,设旋转角为
,设旋转角为 ,记直线
,记直线 与
与 的交点为
的交点为


(1)如图
 ,当
,当 时,线段
时,线段 的长等于 ,线段
的长等于 ,线段 的长等于 .(直接填写结果)
的长等于 .(直接填写结果)(2)如图
 ,当
,当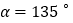 时,求证:
时,求证: ,且
,且 ;
;(3)设
 的中点为
的中点为 ,则线段
,则线段 的长为 (直接填写结果).
的长为 (直接填写结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】课本拓展
旧知新意:
我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
尝试探究

(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
初步应用:
(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=130°,则∠2-∠C=______;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案______.
3拓展提升:
(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需要说明理由)
-
科目: 来源: 题型:
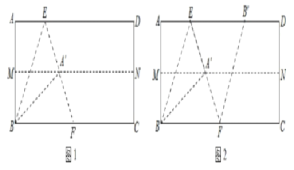
查看答案和解析>>【题目】对一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图1;
第三步:再沿EA′所在的直线折叠,点B落在AD的点B′处,得到折痕EF,同时得到线段B′F,展开,如图2.
(1)证明:∠ABE=30°;
(2)证明:四边形BFB′E为菱形.
-
科目: 来源: 题型:
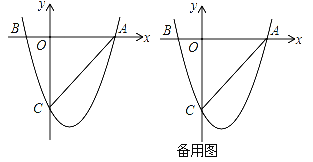
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣3)
(1)求该二次函数的解析式;
(2)设E是y轴右侧抛物线上异于点A的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH,则在点E的运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)设P点是x轴下方的抛物线上的一个动点,连接PA、PC,求△PAC面积的取值范围,若△PAC面积为整数时,这样的△PAC有几个?
相关试题

