【题目】如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,且AE=DE.
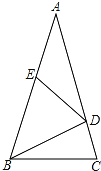
(1)写出图中三对相似比不为1的相似三角形 .
(2)选择(1)中一对加以证明.
参考答案:
【答案】(1)△ABC∽△BDC,△ABC∽△BDE,△EAD∽△DAB.(2)见解析
【解析】
试题分析:(1)利用等腰三角形的性质和三角形的内角和定理可计算出图中所有角的度数,然后根据有两组角对应相等的两个三角形相似可判断△ABC∽△BDC,△ABC∽△BDE,△EAD∽△DAB;
(2)利用等腰三角形的性质和三角形的内角和定理可计算出∠ABC=∠C=72°,再由BD为角平分线得到∠CBD=36°,于是根据有两组角对应相等的两个三角形相似可判断△ABC∽△BDC.
解:(1)△ABC∽△BDC,△ABC∽△BDE,△EAD∽△DAB.
故答案为△ABC∽△BDC,△ABC∽△BDE,△EAD∽△DAB.
(2)△ABC∽△BDC.理由如下:
∵AB=AC,∠A=36°,
∴∠ABC=∠C=![]() (180°﹣36°)=72°,
(180°﹣36°)=72°,
∵BD为角平分线,
∴∠CBD=36°,
∴∠A=∠CBD,∠BCD=∠ACB,
∴△ABC∽△BDC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.

(1)如图1,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为 .
(2)不改变图1中灯泡的高度,将两个边长为30cm的正方形框架按图2摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(3)有n个边长为a的正方形按图3摆放,测得横向影子A′B,D′C的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四种图形都是轴对称图形,其中对称轴条数最多的图形是
A. 等边三角形 B. 矩形 C. 菱形 D. 正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直线y=3x向上平移1个单位,可以得到直线 .
-
科目: 来源: 题型:
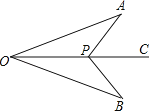
查看答案和解析>>【题目】如图,点P是∠AOB的角平分线OC上一点,分别连接AP、BP,若再添加一个条件即可判定△AOP≌△BPO,则一下条件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC; ④AP=BP;⑤OA=OB.其中一定正确的是 (只需填序号即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋中装有红、黄、白三种颜色球共100个,它们除颜色外都相同,其中黄球个数是白球个数的2倍少5个.已知从袋中摸出一个球是红球的概率是
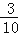 .
.(1)求袋中红球的个数;
(2)求从袋中摸出一个球是白球的概率;
(3)取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等式(﹣a﹣b)( )=a2﹣b2中,括号里应填的多项式是( )
A. a﹣b B. a+b C. ﹣a﹣b D. b﹣a
相关试题

