【题目】已知:线段AB=20cm.
(1)如图1,点P沿线段AB自A点向B点以2厘米/秒运动,点P出发2秒后,点Q沿线段BA自B点向A点以3厘米/秒运动,问再经过几秒后P、Q相距5cm?
(2)如图2:AO=4厘米,PO=2厘米,∠POB=60°,点P绕着点O以60°/秒的速度逆时针旋转一周停止,同时点Q沿直线BA自B点向A点运动,假若点P、Q两点能相遇,求点Q运动的速度.

参考答案:
【答案】(1)经过![]() s或
s或![]() s后,点P、Q相距5cm.(2)点Q的速度为9cm/s或2.8cm/s.
s后,点P、Q相距5cm.(2)点Q的速度为9cm/s或2.8cm/s.
【解析】
试题分析:(1)设经过xs,P、Q两点相距5cm,分相遇前和相遇后两种情况建立方程求出其解即可;
(2)由于点P,Q只能在直线AB上相遇,而点P旋转到直线AB上的时间分两种情况,所以根据题意列出方程分别求解.
试题解析:(1)设再经过ts后,点P、Q相距5cm,
①P、Q未相遇前相距5cm,依题意可列
2(t+2)+3t=20-5,解得,t=![]() ,
,
②P、Q相遇后相距5cm,依题意可列
2(t+2)+3t=20+5,解得,t=![]() ,
,
答:经过![]() s或
s或![]() s后,点P、Q相距5cm.
s后,点P、Q相距5cm.
(2)点P,Q只能在直线AB上相遇,则点P旋转到直线AB上的时间为![]() =2s
=2s
或![]() =5s
=5s
设点Q的速度为ym/s,
当2秒时相遇,依题意得,2y=20-2=18,解得y=9
当5秒时相遇,依题意得,5y=20-6=14,解得y=2.8
答:点Q的速度为9cm/s或2.8cm/s.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
求证:四边形ADCF是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:(1)2x-5=3x+2;
(2)3(x+2)-2(2x-3)=12;
(3)
 -
- =1.
=1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(7,3),点E在边AB上,且AE=1,已知点P为y轴上一动点,连接EP,过点O作直线EP的垂线段,垂足为点H,在点P从点F(0,
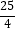 )运动到原点O的过程中,点H的运动路径长为 .
)运动到原点O的过程中,点H的运动路径长为 . 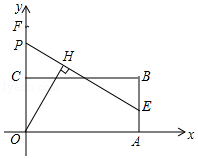
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是生活中常见的月历的示意图,请结合图示回答下列问题.
一
二
三
四
五
六
日
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
(1)如图是另一个月的月历,a表示该月中某一天,b,c,d是该月中其他3天,b,c,d分别与a的关系:b=________;c=________;d=________(用含a的代数式填空).
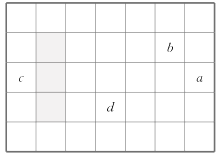
(2)用一个长方形框圈出月历中的三个数(如 图中的阴影),若这三个数之和等于51,则这三个数分别是多少?
(3)这样圈出的三个数的和可能是64吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)求证:四边形ADCE是矩形;
(2)当△ABC满足什么条件时,四边形ADCE是正方形?给出证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为 .
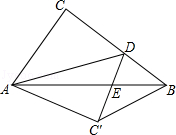
相关试题

