搜索
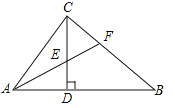
【题目】如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，AF平分∠CAB，交CD于点E，交CB于点F．若AC=3，AB=5，则CE的长为（ ）
A． 
B． 
C． 
D．
参考答案：
【答案】A．
【解析】
试题分析：过点F作FG⊥AB于点G，∵∠ACB=90°，CD⊥AB，∴∠CDA=90°，∴∠CAF+∠CFA=90°，∠FAD+∠AED=90°，∵AF平分∠CAB，∴∠CAF=∠FAD，∴∠CFA=∠AED=∠CEF，∴CE=CF，∵AF平分∠CAB，∠ACF=∠AGF=90°，∴FC=FG，∵∠B=∠B，∠FGB=∠ACB=90°，∴△BFG∽△BAC，∴
，∵AC=3，AB=5，∠ACB=90°，∴BC=4，∴
，∵FC=FG，∴
，解得：FC=
，即CE的长为．故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面的计算不正确的是（ ）
A. 5a3﹣a3=4a3 B. 2m3n=6m+n C. 2m2n=2m+n D. ﹣a2（﹣a3）=a5
-
科目： 来源： 题型：
查看答案和解析>>【题目】某中学开展“汉字听写大赛”活动，为了解学生的参与情况，在该校随机抽取了四个班级学生进行调查，将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图，请根据图中的信息，解答下列问题：
（1）这四个班参与大赛的学生共__________人；
（2）请你补全两幅统计图；
（3）求图1中甲班所对应的扇形圆心角的度数；
（4）若四个班级的学生总数是160人，全校共2000人，请你估计全校的学生中参与这次活动的大约有多少人.
-
科目： 来源： 题型：
查看答案和解析>>【题目】分解因式：
（1）5mx2﹣10mxy+5my2
（2）4（a﹣b）2﹣（a+b）2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC与△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点D在AB上，点E与点C在AB的两侧，连接BE，CD，点M、N分别是BE、CD的中点，连接MN，AM，AN．
下列结论：①△ACD≌△ABE；②△ABC∽△AMN；③△AMN是等边三角形；④若点D是AB的中点，则S△ABC=2S△ABE．
其中正确的结论是 ．（填写所有正确结论的序号）
-
科目： 来源： 题型：
查看答案和解析>>【题目】分解因式：（a2+2a）2﹣7（a2+2a）﹣8．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知多项式kx2-6xy-8y2可写成（2mx+2y）(x-4y)的形式，求k，m的值．
相关试题
