【题目】如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是

A.①②③ B.①②④ C.②③④ D.①②③④
参考答案:
【答案】B
【解析】
试题∵四边形ABCD是矩形,∴∠D=∠BCD=90°,DF=MF。
由折叠的性质可得:∠EMF=∠D=90°,即FM⊥BE,CF⊥BC。
∵BF平分∠EBC,∴CF=MF。∴DF=CF。故①正确。
∵∠BFM=90°﹣∠EBF,∠BFC=90°﹣∠CBF,∴∠BFM=∠BFC。
∵∠MFE=∠DFE=∠CFN,∴∠BFE=∠BFN。
∵∠BFE+∠BFN=180°,∴∠BFE=90°,即BF⊥EN。故②正确。
∵在△DEF和△CNF中,易由ASA得△DEF≌△CNF,∴EF=FN。∴BE=BN。
但无法求得△BEN各角的度数,
∴△BEN不一定是等边三角形。故③错误。
∵∠BEM=∠BFC,BM⊥FM,BC⊥CF,∴BM=BC=AD=2DE=2EM。∴BM=3EM。
∴S△BEF=3S△EMF=3S△DEF。故④正确。
综上所述,正确的结论是①②④。故选B。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,射线
,射线 分别和直线
分别和直线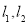 交于点
交于点 ,射线
,射线 分别和直线
分别和直线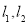 交于点
交于点 .点
.点 在
在 上(
上( 点与
点与 三点不重合).连接
三点不重合).连接 .请你根据题意画出图形并用等式直接写出
.请你根据题意画出图形并用等式直接写出 、
、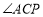 、
、 之间的数量关系.
之间的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】有四张规格、质地相同的卡片,它们背面完全相同,正面图案分别是A 菱形,B 平行四边形,C 线段,D 角,将这四张卡片背面朝上洗匀后
(1)随机抽取一张卡片图案是轴对称图形的概率是 ;
(2)随机抽取两张卡片(不放回),求两张卡片卡片图案都是中心对称图形的概率,并用树状图或列表法加以说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为

A.
 B.3 C.1 D.
B.3 C.1 D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为_____.

-
科目: 来源: 题型:
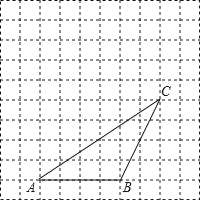
查看答案和解析>>【题目】如图,网格中每个小正方形边长为1,△ABC的顶点都在格点(网格线的交点)上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′;
(3)若连接BB′,CC′,则这两条线段的关系是_______;
(4)△ABC的面积为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解读基础:
(1)图1形似燕尾,我们称之为“燕尾形”,请写出
 、
、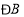 、
、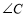 、
、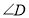 之间的关系,并说明理由;
之间的关系,并说明理由;(2)图2形似8字,我们称之为“八字形”,请写出
 、
、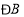 、
、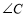 、
、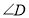 之间的关系,并说明理由:
之间的关系,并说明理由:应用乐园:直接运用上述两个结论解答下列各题
(3)①如图3,在
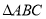 中,
中, 、
、 分别平分
分别平分 和
和 ,请直接写出
,请直接写出 和
和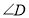 的关系 ;
的关系 ;②如图4,
 .
.(4)如图5,
 与
与 的角平分线相交于点
的角平分线相交于点 ,
,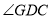 与
与 的角平分线相交于点
的角平分线相交于点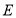 ,已知
,已知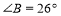 ,
, ,求
,求 和
和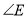 的度数.
的度数.
相关试题

