【题目】解读基础:
(1)图1形似燕尾,我们称之为“燕尾形”,请写出![]() 、
、![]() 、
、![]() 、
、![]() 之间的关系,并说明理由;
之间的关系,并说明理由;
(2)图2形似8字,我们称之为“八字形”,请写出![]() 、
、![]() 、
、![]() 、
、![]() 之间的关系,并说明理由:
之间的关系,并说明理由:
应用乐园:直接运用上述两个结论解答下列各题
(3)①如图3,在![]() 中,
中,![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,请直接写出
,请直接写出![]() 和
和![]() 的关系 ;
的关系 ;
②如图4,![]() .
.
(4)如图5,![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,
,![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,已知
,已知![]() ,
,![]() ,求
,求![]() 和
和![]() 的度数.
的度数.

参考答案:
【答案】(1)![]() ,理由详见解析;(2)
,理由详见解析;(2)![]() ,理由详见解析:(3)①
,理由详见解析:(3)①![]() ;②360°;(4)
;②360°;(4)![]() ;
; ![]() .
.
【解析】
(1)根据三角形外角等于不相邻的两个内角之和即可得出结论;
(2)根据三角形内角和定理及对顶角相等即可得出结论;
(3)①根据角平分线的定义及三角形内角和定理即可得出结论;
②连结BE,由(2)的结论及四边形内角和为360°即可得出结论;
(4)根据(1)的结论、角平分线的性质以及三角形内角和定理即可得出结论.
(1)![]() .理由如下:
.理由如下:
如图1,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)![]() .理由如下:
.理由如下:
在![]() 中,
中,![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ;
;
(3)①![]() ,
,![]() ,
,![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,
,![]()
![]() ,
,![]() .
.
故答案为:![]() .
.
②连结![]() .
.
∵![]() ,
,![]() .
.
故答案为:![]() ;
;

(4)由(1)知,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是

A.①②③ B.①②④ C.②③④ D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为_____.

-
科目: 来源: 题型:
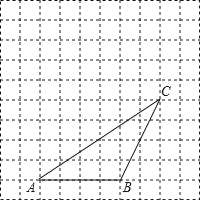
查看答案和解析>>【题目】如图,网格中每个小正方形边长为1,△ABC的顶点都在格点(网格线的交点)上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′;
(3)若连接BB′,CC′,则这两条线段的关系是_______;
(4)△ABC的面积为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次考试中,某班级的数学成绩统计图如图.下列说法错误的是( )

A. 得分在70~80分之间的人数最多 B. 该班的总人数为40
C. 得分在90~100分之间的人数最少 D. 及格(≥60分)人数是26
-
科目: 来源: 题型:
查看答案和解析>>【题目】四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:
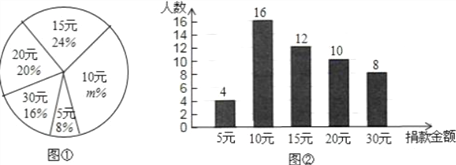
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分8分)如图,点E、F为线段BD的两个三等分点,四边形AECF是菱形.

(1)试判断四边形ABCD的形状,并加以证明;
(2)若菱形AECF的周长为20,BD为24,试求四边形ABCD的面积.
相关试题

