【题目】已知两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
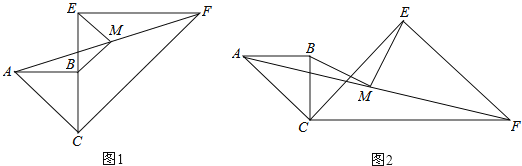
(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;
(2)如图1,若CB=a,CE=2a,求BM,ME的长;
(3)如图2,当∠BCE=45°时,求证:BM=ME.
参考答案:
【答案】(1)证明见解析;(2)BM=ME=![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)如图1,延长AB交CF于点D,证明BM为△ADF的中位线即可.
(2)如图2,作辅助线,推出BM、ME是两条中位线.
(3)如图3,作辅助线,推出BM、ME是两条中位线:BM=![]() DF,ME=
DF,ME=![]() AG;然后证明△ACG≌△DCF,得到DF=AG,从而证明BM=ME.
AG;然后证明△ACG≌△DCF,得到DF=AG,从而证明BM=ME.
(1)如图1,延长AB交CF于点D,则易知△ABC与△BCD均为等腰直角三角形,
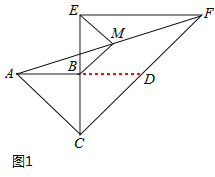
∴AB=BC=BD.
∴点B为线段AD的中点.
又∵点M为线段AF的中点,
∴BM为△ADF的中位线.
∴BM∥CF.
(2)如图2,延长AB交CF于点D,则易知△BCD与△ABC为等腰直角三角形,
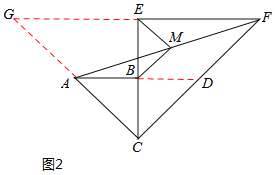
∴AB=BC=BD=a,AC=AD=![]() a,
a,
∴点B为AD中点,又点M为AF中点.
∴BM=![]() DF.
DF.
分别延长FE与CA交于点G,则易知△CEF与△CEG均为等腰直角三角形,
∴CE=EF=GE=2a,CG=CF=![]() a.
a.
∴点E为FG中点,又点M为AF中点.
∴ME=![]() AG.
AG.
∵CG=CF=![]() a,CA=CD=
a,CA=CD=![]() a,∴AG=DF=
a,∴AG=DF=![]() a.
a.
∴BM=ME=![]() .
.
(3)如图3,延长AB交CE于点D,连接DF,则易知△ABC与△BCD均为等腰直角三角形,
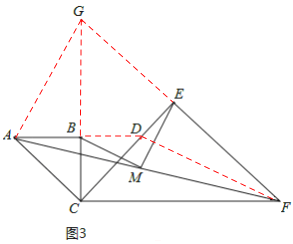
∴AB=BC=BD,AC=CD.
∴点B为AD中点.
又点M为AF中点,∴BM=![]() DF.
DF.
延长FE与CB交于点G,连接AG,则易知△CEF与△CEG均为等腰直角三角形,
∴CE=EF=EG,CF=CG.
∴点E为FG中点.
又点M为AF中点,∴ME=![]() AG.
AG.
在△ACG与△DCF中,∵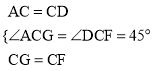 ,
,
∴△ACG≌△DCF(SAS).
∴DF=AG,∴BM=ME.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学数学活动小组为了调查居民的用水情况,从某社区的
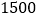 户家庭中随机抽取了
户家庭中随机抽取了 户家庭的月用水量,结果如下表所示:
户家庭的月用水量,结果如下表所示:月用水量(吨)

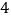




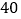
户数
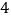



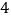
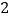

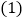 求这
求这 户家庭月用水量的平均数、众数和中位数;
户家庭月用水量的平均数、众数和中位数; 根据上述数据,试估计该社区的月用水量;
根据上述数据,试估计该社区的月用水量;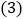 由于我国水资源缺乏,许多城市常利用分段计费的方法引导人们节约用水,即规定每个家庭的月基本用水量为
由于我国水资源缺乏,许多城市常利用分段计费的方法引导人们节约用水,即规定每个家庭的月基本用水量为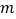 (吨),家庭月用水量不超过
(吨),家庭月用水量不超过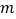 (吨)的部分按原价收费,超过
(吨)的部分按原价收费,超过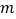 (吨)的部分加倍收费.你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合适?简述理由.
(吨)的部分加倍收费.你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合适?简述理由. -
科目: 来源: 题型:
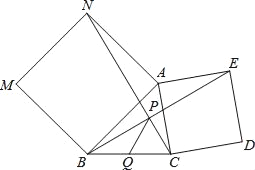
查看答案和解析>>【题目】探究:如图,分别以△ABC的两边AB和AC为边向外作正方形ANMB和正方形ACDE,NC、BE交于点P.
求证:∠ANC=∠ABE.
应用:Q是线段BC的中点,若BC=6,则PQ= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,BC∥OA,BC=3,OA=6,AB=3
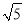 .
.(1)直接写出点B的坐标;
(2)已知D、E(2,4)分别为线段OC、OB上的点,OD=5,直线DE交x轴于点F,求直线DE的解析式;
(3)在(2)的条件下,点M是直线DE上的一点,在x轴上方是否存在另一个点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.

根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是 ;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.
-
科目: 来源: 题型:
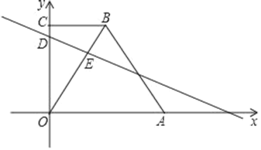
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形ABCD的边BC在x轴的正半轴上,点B在点C的左侧,直线y=kx经过点A(2,2)和点P,且OP=4
 ,将直线y=kx沿y轴向下平移得到直线y=kx+b,若点P落在矩形ABCD的内部,则b的取值范围是( )
,将直线y=kx沿y轴向下平移得到直线y=kx+b,若点P落在矩形ABCD的内部,则b的取值范围是( ) 
A. 0<b<2 B. -2<b<0 C. -4<b<2 D. -4<b<-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)

相关试题

