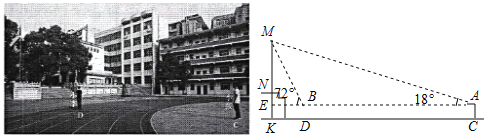
【题目】为了测量学校旗杆的高度,身高相同的小张和小李站在操场如图所示的位置,小张在C处测得旗杆顶端的仰角为18°,小李在D处测得旗杆顶端的仰角为72°,又已知两人之间的距离CD为24米,两人的眼睛离地面的距离AC、BD均为1.6米,旗杆的底部N距离操场所在平面的垂直高度NK=2米,求旗杆MN的高度.(参考数据:tan18°≈![]() .)
.)
参考答案:
【答案】旗杆MN的高度是8.6米.
【解析】试题分析:设ME=x,通过解直角△EBM得到ME的长度,通过解直角△AME得到ME的长度,由此列出方程求得x的值,然后结合图形找到相关线段的和差关系进行解答.
试题解析:设ME=x.
∵在直角△AME中,∠MAE=18°,
∴EM=AEtan18°=![]() AE.即AE=3x;
AE.即AE=3x;
∵在直角△EBM中,∠MBE=72°,
∴ME=BEtan72°=3BE,即BE=![]() ME,
ME,
∴3x-![]() x=24,
x=24,
解得x=9,
∴MK=10.6米,
又NK=2米,
∴MN=10.6-2=8.6(米).
答:旗杆MN的高度是8.6米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】衢州市“十二五”规划纲要指出,力争到2015年,全市农民人均年纯收入超13000元,数13000用科学记数法可以表示为( )
A.13×103
B.1.3×104
C.0.13×104
D.130×102 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学在一次实验中统计了某一结果出现的频率,给出的统计图如图所示,则 符合这一结果的实验可能是( )

A. 掷一枚正六面体的骰子,出现6点的概率
B. 掷一枚硬币,出现正面朝上的概率
C. 任意写出一个整数,能被2整除的概率
D. 一个袋子中装着只有颜色不同,其他都相同的两个红球和一个黄球,从中任意取出一个是黄球的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:(2a-3)(2a+3)-(a-1)2=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在九年级体育中考中,某校某班参加仰卧起坐测试的一组女生(每组8人)测试成绩如下(单位:次/分):44,45,42,48,46,43,47,45.则这组数据的极差为( )
A.2
B.4
C.6
D.8 -
科目: 来源: 题型:
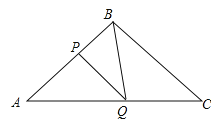
查看答案和解析>>【题目】如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒。
(1)当x为何值时,PQ∥BC?
(2)当
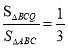 时,求
时,求 的值;
的值;(3)△APQ能否与△CQB相似?若能,求出时间x的值,若不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似地,可以在等腰三角形中建立边角之间的关系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad)如图1,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad
 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解答下列问题:
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解答下列问题:(1)sad
 = ;
= ;(2)对于
 <A<
<A< ,∠A的正对值sadA的取值范围 ;
,∠A的正对值sadA的取值范围 ;(3如图2,已知sinA=
 ,其中∠A为锐角,试求sadA的值。
,其中∠A为锐角,试求sadA的值。

相关试题

