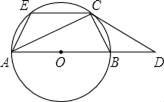
【题目】已知:如图,AB是⊙O的直径,C是⊙O上一点,过C点的切线与AB的延长线交于点D,CE∥AB交⊙O于点E,连接AC、BC、AE.
(1)求证:①∠DCB=∠CAB;②CDCE=CBCA;
(2)作CG⊥AB于点G.若tan∠CAB=![]() (k>1),求
(k>1),求![]() 的值(用含k的式子表示).
的值(用含k的式子表示).
参考答案:
【答案】(1)见解析;(2)![]()
【解析】分析:(1)①过点C作直径CF,连接BF.即可得![]() 又由直径所对的圆周角等于直角,可得
又由直径所对的圆周角等于直角,可得![]() 又由切线的性质,可得
又由切线的性质,可得![]() 是直角,即可证得
是直角,即可证得![]() ②由EC∥AB,易证得∠4=∠3=∠BCD.有圆的内接四边形的对角互补,可得∠CBD=∠AEC.即可证得
②由EC∥AB,易证得∠4=∠3=∠BCD.有圆的内接四边形的对角互补,可得∠CBD=∠AEC.即可证得![]() 则得到
则得到![]()
(2)在![]() 与
与![]() 中,利用三角函数的性质,即可求得
中,利用三角函数的性质,即可求得![]() 的值.
的值.
详解:(1)证明:①如图1,
作直径CF,连接BF.
∴![]()
则![]()
∵CD切![]() 于C,
于C,
∴OC⊥CD,
则![]()
∴∠BCD=∠CAB.
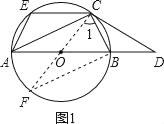
②∵EC∥AB,∠BCD=∠3,
∴∠4=∠3=∠BCD.
∵![]()
∵![]()
∴∠CBD=∠AEC.
∴△ACE∽△DCB.
∴![]()
∴CDCE=CBCA.
(2)如图2,连接EB,交OC于点H,
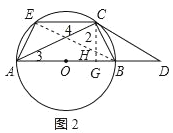
∵CG⊥AB于点G,![]()
∴∠3=∠BCG.
∴AE=BC,
∵∠3=∠4.
∴∠3=∠EBG.
∴∠BCG=∠EBG.
∵![]()
∴在Rt△HGB中,![]()
在Rt△BCG中,![]()
设HG=a,则![]()
∵EC∥AB,
∴△ECH∽△BGH.
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx经过点A(﹣1,
 )及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.
)及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.(1)求抛物线的解析式;
(2)如图1,连接AO、BO,若△OAB的面积为5,求m的值;
(3)如图2,作BE⊥x轴于E,连接AC、DE,当D点运动变化时,AC、DE的位置关系是否变化?请证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为12cm,点B,D之间的距离为16m,则线段AB的长为
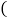
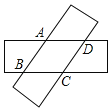
A.
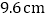 B. 10cmC. 20cmD. 12cm
B. 10cmC. 20cmD. 12cm -
科目: 来源: 题型:
查看答案和解析>>【题目】一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算,若租两车合运,10天可以完成任务,若甲车的效率是乙车效率的2倍.
 甲、乙两车单独完成任务分别需要多少天?
甲、乙两车单独完成任务分别需要多少天? 已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元
已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元 试问:租甲乙车两车、单独租甲车、单独租乙车这三种方案中,哪一种租金最少?请说明理由.
试问:租甲乙车两车、单独租甲车、单独租乙车这三种方案中,哪一种租金最少?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一面靠墙的空地上,用长为24米的篱笆围成中间隔有二道篱笆的长方形花圃,从设计的美观角度出发,墙的最小可用长度为4米,墙的最大可用长度为14米.
(1)若所围成的花圃的面积为32平方米,求花圃的宽AB的长度;
(2)当AB的长为 时,所围成的花圃面积最大,最大值为 米2;当AB的长为 时,所围成的花圃面积最小,最小值为 米2.

相关试题

