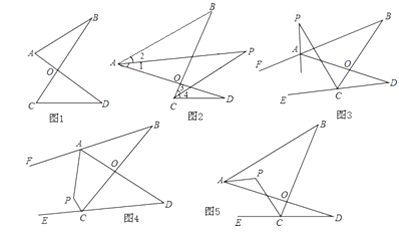
【题目】根据题意解答:(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D.
(2)阅读下面的内容,并解决后面的问题: 如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.
解:∵AP、CP分别平分∠BAD、∠BCD
∴∠1=∠2,∠3=∠4
由(1)的结论得:∠P+∠3=∠1+∠B①,∠P+∠2=∠4+∠D②,①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P= ![]() (∠B+∠D)=26°.
(∠B+∠D)=26°.
①如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
②在图4中,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
③在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
参考答案:
【答案】(1)证明见解析;(2)①∠P=26゜;②∠P=180°﹣![]() (∠B+∠D);③∠P=90°+
(∠B+∠D);③∠P=90°+ ![]() (∠B+∠D).
(∠B+∠D).
【解析】试题分析:(1)根据三角形的内角和等于180°列式整理即可得证;
(2)根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据(1)的结论列出整理即可得解;①表示出∠PAD和∠PCD,再根据(1)的结论列出等式并整理即可得解;
②根据四边形的内角和等于360°,可得(180°﹣∠1)+∠P+∠4+∠B=360°,∠2+∠P+(180°﹣∠3)+∠D=360°,然后整理即可得解;
③根据(1)的结论∠B+∠BAD=∠D+∠BCD,∠PAD+∠P=∠D+∠PCD,然后整理即可得解.
试题解析:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180゜, ∴∠A+∠B+∠AOB=∠C+∠D+∠COD.∵∠AOB=∠COD,∴∠A+∠B=∠C+∠D.
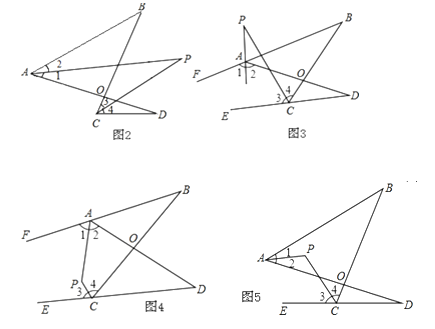
(2)①∠P=26゜.∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,∴∠1=∠2,∠3=∠4.由(1)的结论得:∠PAD+∠P=∠PCD+∠D ①,∠PAB+∠P=∠PCB+∠B ②,∵∠PAB=∠1,∠1=∠2,∴∠PAB=∠2,∴∠2+∠P=∠3+∠B ③,①+③得∠2+∠P+∠PAD+∠P=∠3+∠B+∠PCD+∠D,即2∠P+180°=∠B+∠D+180°,∴∠P=![]() (∠B+∠D )=26°.
(∠B+∠D )=26°.
②如图4,∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,∴∠1=∠2,∠3=∠4,∴(180°﹣2∠1)+∠B=(180°﹣2∠4)+∠D,在四边形APCB中,(180°﹣∠1)+∠P+∠4+∠B=360°,在四边形APCD中,∠2+∠P+(180°﹣∠3)+∠D=360°,∴2∠P+∠B+∠D=360°,∴∠P=180°﹣![]() (∠B+∠D);
(∠B+∠D);
③如图5,∵AP平分∠BAD,CP平分∠BCD的外角∠BCE,∴∠1=∠2,∠3=∠4,∵(∠1+∠2)+∠B=(180°﹣2∠3)+∠D,∠2+∠P=(180°﹣∠3)+∠D,![]() (∠B+∠D).
(∠B+∠D).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AC=BC,∠ACB=90°,CE是过C点的一条直线,AD⊥CE于D,BE⊥CE于E,DE=4cm,AD=2cm,则BE=( )
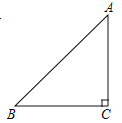
A. 2cm B. 4cm C. 6cm或2cm D. 6cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在图 (每个小正方形的边长均为1)中建立两个不同的平面直角坐标系,在各个坐标系中分别写出六边形6个顶点的坐标;
(2)要使图中点B与点F的横坐标互为相反数,则应选取怎样的直线作为y轴,试在图中标出来,此时点E与点C的横坐标有什么关系?

-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节前夕,小东的父母准备购买若干个粽子和咸鸭蛋(每个粽子的价格相同,每个咸鸭蛋的价格相同).已知粽子的价格比咸鸭蛋的价格贵1.8元,花30元购买粽子的个数与花12元购买咸鸭蛋的个数相同,求粽子与咸鸭蛋的价格各多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验与探究:
(
 )如图,直线
)如图,直线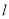 为第一、三象限的角平分线,观察易知
为第一、三象限的角平分线,观察易知 关于直线
关于直线 的对称点
的对称点 的坐标为
的坐标为 ,请在图中分别标明
,请在图中分别标明 、
、 关于直线
关于直线 的对称点
的对称点 、
、 的位置,并写出他们的坐标:
的位置,并写出他们的坐标:  __________、
__________、 __________.
__________.(
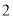 )结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点
)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点 关于第一、三象限的角平分线
关于第一、三象限的角平分线 的对称点
的对称点 的坐标为__________ (不必证明).
的坐标为__________ (不必证明).(
 )已知两点
)已知两点 、
、 ,在直线
,在直线 上是否存在一点
上是否存在一点 ,使点
,使点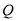 到
到 、
、 两点的距离之和最小,并求出最小距离.
两点的距离之和最小,并求出最小距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,
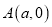 ,
, 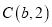 ,且满足
,且满足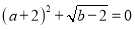 ,过
,过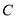 作
作 轴于
轴于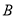 .
.(
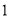 )求
)求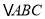 的面积.
的面积.(
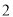 )在
)在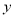 轴上是否存在点
轴上是否存在点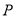 ,使
,使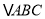 和
和 的面积相等?若存在,求出
的面积相等?若存在,求出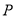 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.(
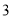 )动点
)动点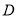 从点
从点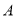 出发,以每秒
出发,以每秒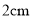 的速度沿射线
的速度沿射线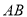 运动,如果在运动过程中
运动,如果在运动过程中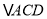 为等腰三角形,求出点
为等腰三角形,求出点 运动的时间.
运动的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校7年级的学生从学校O点出发,要到某地P处进行探险活动,他们先向正西方向走8km到A处,又往正南方向走4km到B处,又折向正东方向走6km到C处,再折向正北方向走8km到D处,最后又往正东方向走4km才到探险地P;取点O为原点,取点O的正东方向为x轴的正方向,取点O的正北方向为y轴的正方向,以2km为一个单位长度建立平面直角坐标系.

(1)在平面直角坐标系中画出探险路线图;
(2)分别写出A、B、C、D、P点的坐标.
相关试题

