【题目】如图,在平面直角坐标系中,经过点A的双曲线y=![]() (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为_____.
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为_____.

参考答案:
【答案】![]()
【解析】分析:过A作AM⊥y轴于M,过B作BD选择x轴于D,直线BD与AM交于点N,则OD=MN,DN=OM,∠AMO=∠BNA=90°,由等腰三角形的判定与性质得出OA=BA,∠OAB=90°,证出∠AOM=∠BAN,由AAS证明△AOM≌△BAN,得出AM=BN=1,OM=AN=k,求出B(1+k,k﹣1),得出方程(1+k)(k﹣1)=k,解方程即可.
详解:如图所示,过A作AM⊥y轴于M,过B作BD选择x轴于D,直线BD与AM交于点N,
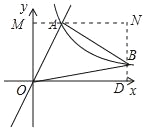
则OD=MN,DN=OM,∠AMO=∠BNA=90°,
∴∠AOM+∠OAM=90°,
∵∠AOB=∠OBA=45°,
∴OA=BA,∠OAB=90°,
∴∠OAM+∠BAN=90°,
∴∠AOM=∠BAN,
∴△AOM≌△BAN,
∴AM=BN=1,OM=AN=k,
∴OD=1+k,BD=OM﹣BN=k﹣1
∴B(1+k,k﹣1),
∵双曲线y=![]() (x>0)经过点B,
(x>0)经过点B,
∴(1+k)(k﹣1)=k,
整理得:k2﹣k﹣1=0,
解得:k=![]() (负值已舍去),
(负值已舍去),
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
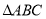 中,
中, 、
、 分别垂直平分
分别垂直平分 和
和 ,交
,交 于
于 、
、 两点,
两点, 与
与 相交于点
相交于点 .
.
(1)若
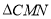 的周长为15 cm,求
的周长为15 cm,求 的长.
的长.(2)若
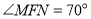 ,求
,求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙二人同时从A地出发,沿同一条道路去B地,途中都使用两种不同的速度Vl与V2(Vl<V2),甲用一半的路程使用速度Vl、另一半的路程使用速度V2;乙用一半的时间使用速度Vl、另一半的时间使用速度V2;关于甲乙二人从A地到达B地的路程与时间的函数图象及关系,有图中4个不同的图示分析.其中横轴t表示时间,纵轴s表示路程,其中正确的图示分析为( )

A. 图(1) B. 图(1)或图(2) C. 图(3) D. 图(4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 中,
中, ,
, ,
, ,
, ,动点
,动点 从点
从点 出发,沿着
出发,沿着 的三条边逆时针走一圈回到
的三条边逆时针走一圈回到 点,速度为2
点,速度为2 ,设运动时间为
,设运动时间为 秒.
秒.(1)
 时,
时, 为等腰三角形?
为等腰三角形?(2)另有一点
 从点
从点 开始,按顺时针走一圈回到
开始,按顺时针走一圈回到 点,且速度为每秒3cm,若
点,且速度为每秒3cm,若 、
、 两点同时出发,当
两点同时出发,当 、
、 中有一点到达终点时,另一点也停止运动.当
中有一点到达终点时,另一点也停止运动.当 为何值时,直线
为何值时,直线 把
把 的周长分成相等的两部分?
的周长分成相等的两部分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以正方形ABCD的边AD为一边作等边三角形ADE,F是DE的中点,BE、AF相交于点G,连接DG,若正方形ABCD的面积为36,则BG=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果一条线段将一个三角形分成2个小等腰三角形,我们把这条线段叫做这个三角形的“好线”:如果两条线段将一个三角形分成3个小等腰三角形,我们把这两条线段叫做这个三角形的“好好线”.
理解:
(1)如图1,在
 中,
中, ,点
,点 在
在 边上,且
边上,且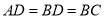 ,求
,求 的大小;
的大小;(2)在图1中过点
 作一条线段
作一条线段 ,使
,使 ,
, 是
是 的“好好线”;
的“好好线”;在图2中画出顶角为
 的等腰三角形的“好好线”,并标注每个等腰三角形顶角的度数(画出一种即可);
的等腰三角形的“好好线”,并标注每个等腰三角形顶角的度数(画出一种即可);应用:
(3)在
 中,
中, ,
, 和
和 是
是 的“好好线”,点
的“好好线”,点 在
在 边上,点
边上,点 在
在 边上,且
边上,且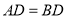 ,
, ,请求出
,请求出 的度数.
的度数.
相关试题

