【题目】定义：如果一条线段将一个三角形分成2个小等腰三角形，我们把这条线段叫做这个三角形的“好线”：如果两条线段将一个三角形分成3个小等腰三角形，我们把这两条线段叫做这个三角形的“好好线”.

理解：

（1）如图1，在中，，点在边上，且，求的大小；

（2）在图1中过点作一条线段，使，是的“好好线”；

在图2中画出顶角为的等腰三角形的“好好线”，并标注每个等腰三角形顶角的度数（画出一种即可）；

应用：

（3）在中，，和是的“好好线”，点在边上，点在边上，且，，请求出的度数.

参考答案：

【答案】（1）36°；（2）见详解；（3）18°或42°

【解析】

（1）利用等边对等角得到三对角相等，设∠A=∠ABD=x，表示出∠BDC与∠C，列出关于x的方程，求出方程的解得到x的值，即可确定出∠A的度数．
（2）根据（1）的解题过程作出△ABC的“好好线”；45°自然想到等腰直角三角形，过底角一顶点作对边的高，发现形成一个等腰直角三角形和直角三角形．直角三角形斜边的中线可形成两个等腰三角形；第二种情形以一底角作为新等腰三角形的底角，则另一底角被分为45°和22.5°，再以22.5°分别作为等腰三角形的底角或顶角，易得其中作为底角时所得的三个三角形恰都为等腰三角形；
（3）用量角器，直尺标准作27°角，而后确定一边为BA，一边为BC，根据题意可以先固定BA的长，而后可确定D点，再分别考虑AD为等腰三角形的腰或者底边，兼顾A、E、C在同一直线上，易得2种三角形ABC；根据图形易得∠C的值；

解：（1）∵AB=AC，
∴∠ABC=∠C，
∵BD=BC=AD，
∴∠A=∠ABD，∠C=∠BDC，
设∠A=∠ABD=x，则∠BDC=2x，∠C=

可得

∴x=36°

则∠A=36°；

（2）如图所示：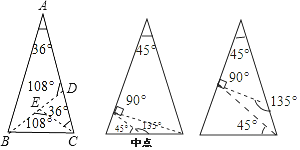

（3）如图所示：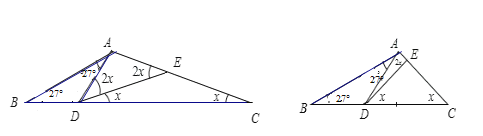

①当AD=AE时，
∵2x+x=27°+27°，
∴x=18°；
②当AD=DE时，
∵27°+27°+2x+x=180°，
∴x=42°；
综上所述，∠C为18°或42°的角．

关闭