【题目】如图,△ABC中,AB=AC,以AC为斜边作Rt△ADC,使∠ADC=90°,∠CAD=∠CAB=26°,E、F分别是BC、AC的中点,则∠EDF等于°. 
参考答案:
【答案】51
【解析】解:∵E、F分别是BC、AC的中点,∠CAD=∠CAB=26°, ∴EF是△ABC的中位线,
∴EF= ![]() AB,∠EFC=∠CAB=26°.
AB,∠EFC=∠CAB=26°.
∵AB=AC,△ACD是直角三角形,点E是斜边AC的中点,
∴DF=AF=CF,
∴DF=EF,∠CAD=∠ADF=26°.
∵∠DFC是△AFD的外角,
∴∠DFC=26°+26°=52°,
∴∠EFD=∠EFC+∠DFC=26°+52°=78°,
∴∠EDF= ![]() =51°.
=51°.
所以答案是:51.
【考点精析】根据题目的已知条件,利用直角三角形斜边上的中线和三角形中位线定理的相关知识可以得到问题的答案,需要掌握直角三角形斜边上的中线等于斜边的一半;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:(15x3y+10x2y﹣5xy2)÷5xy
(2)计算:(3x+y)(x+2y)﹣3x(x+2y)
(3)先化简,再求值:(x+2)(x﹣2)﹣(x+1)2,其中x=
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC的平分线AD交BC于点D,DE垂直平分AC,垂足为点E,∠BAD=29°,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为弘扬“敬老爱老”传统美德,某校八年级(1)班的学生要去距离学校10km的敬老院看望老人,一部分学生骑自行车先走,过了20min后,其余学生乘汽车出发,结果乘汽车的同学早到10min.已知汽车的速度是骑车学生的4倍,求骑车学生的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学体育组因教学需要本学期购进篮球和排球共100个,共花费2600元,已知篮球的单价是20元
 个,排球的单价是30元
个,排球的单价是30元 个.
个. 篮球和排球各购进了多少个
篮球和排球各购进了多少个 列方程组解答
列方程组解答 ?
? 因该中学秋季开学成立小学部,教学资源实现共享,体育组提出还需购进同样的篮球和排球共30个,但学校要求花费不能超过800元,那么排球最多能购进多少个
因该中学秋季开学成立小学部,教学资源实现共享,体育组提出还需购进同样的篮球和排球共30个,但学校要求花费不能超过800元,那么排球最多能购进多少个 列不等式解答
列不等式解答 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】有许多代数恒等式可以用图形的面积来表示,如图
 ,它表示了
,它表示了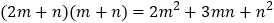
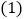 图
图 是将一个长2m、宽2n的长方形,沿图中虚线平方为四块小长方形,然后再拼成一个正方形
是将一个长2m、宽2n的长方形,沿图中虚线平方为四块小长方形,然后再拼成一个正方形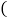 图
图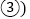 ,则图
,则图 中的阴影部分的正方形的边长等于______
中的阴影部分的正方形的边长等于______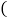 用含m、n的代数式表示
用含m、n的代数式表示
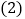 请用两种不同的方法列代数式表示图
请用两种不同的方法列代数式表示图 中阴影部分的面积.
中阴影部分的面积.方法
 ______方法
______方法 ______
______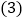 请你观察图形
请你观察图形 ,写出三个代数式
,写出三个代数式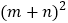 、
、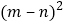 、mn关系的等式:______;
、mn关系的等式:______; 根据
根据 题中的等量关系,解决如下问题:若已知
题中的等量关系,解决如下问题:若已知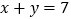 ,
,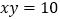 ,则
,则 ______;
______; 小明用8个一样大的长方形
小明用8个一样大的长方形 长acm,宽
长acm,宽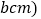 拼图,拼出了如图甲、乙的两种图案,图案甲是一个正方形,图案乙是一个大的长方形,图案甲的中间留下了边长是2cm的正方形小洞
拼图,拼出了如图甲、乙的两种图案,图案甲是一个正方形,图案乙是一个大的长方形,图案甲的中间留下了边长是2cm的正方形小洞 则
则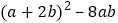 的值为______.
的值为______.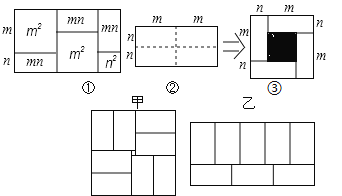
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起
 其中,
其中, ,
, ;
; :
: 若
若 ,则
,则 的度数为______;
的度数为______; 若
若 ,求
,求 的度数;
的度数; 由
由 猜想
猜想 与
与 的数量关系,并说明理由.
的数量关系,并说明理由. 当
当 且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出
且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出 角度所有可能的值
角度所有可能的值 不必说明理由
不必说明理由 ,若不存在,请说明理由.
,若不存在,请说明理由.
相关试题

