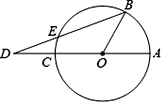
【题目】如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )
A. DE=EB B. ![]() DE=EB C.
DE=EB C. ![]() DE=DO D. DE=OB
DE=DO D. DE=OB
参考答案:
【答案】D
【解析】试题解析:连接EO.

∵OB=OE,
∴∠B=∠OEB,
∵∠OEB=∠D+∠DOE,∠AOB=3∠D,
∴∠B+∠D=3∠D,
∴∠D+∠DOE+∠D=3∠D,
∴∠DOE=∠D,
∴ED=EO=OB,
故选D.
A、错误.假设DE=EB,则△EOB是等边三角形,则∠AOB=3∠D=90°,OB⊥AD,显然与题目不符.
B、错误.假设![]() DE=EB,则△EOB是等腰直角三角形,则∠AOB=3∠D=67.5°,显然与题目不符.
DE=EB,则△EOB是等腰直角三角形,则∠AOB=3∠D=67.5°,显然与题目不符.
C、错误.假设![]() DE=EB,则△EOB是等腰三角形,且底角∠B=30°,则∠AOB=45°,显然不符合题意.
DE=EB,则△EOB是等腰三角形,且底角∠B=30°,则∠AOB=45°,显然不符合题意.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长方形的周长为10,它的长是a,那么它的宽是( )
A.10﹣a
B.10﹣2a
C.5﹣a
D.5﹣2a -
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富同学们的课余生活,某学校举行“亲近大自然”户外活动,现在随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学生只能从“A(植物园),B(花卉园),C(湿地公园),D(森林公园)”四个景点中选择一项,根据调查结果绘制了如下两幅不完整的统计图.
请根据以上信息回答下列问题:
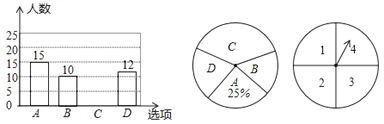
(1)本次调查的样本容量是 ,并补全条形统计图;
(2)若该学校共有3600名学生,试估计该校最想去森林公园的学生人数;(3)从选项为“D(森林公园)”的学生中抽取了小明和小军两人做游戏,游戏规则如下:每人从1,2,…,8中任意选择一个数字,然后两人各转动一次如图所示的转盘(转盘被分为面积相等的四个扇形),两人转出的数字之和等于谁选择的数,谁就获胜;若小军选择的数是5,用列表或画树状图的方法求他获胜的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a<﹣1,则方程x2+(1﹣2a)x+a2=0根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实根
C.没有实数根
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a ≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
①a﹣b+c>0; ②3a+b=0; ③b2=4a(c﹣n); ④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣1,y1)、B(2,y2)、C(﹣3,y3)在函数y=﹣2(x+1)2+3的图象上,则y1、y2、y3的大小关系是( )
A.y1<y2<y3
B.y1<y3<y2
C.y2<y3<y1
D.y3<y2<y1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
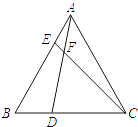
(1)求证:AD=CE;
(2)求∠DFC的度数.
相关试题

