搜索
【题目】如图，我校一块边长为2x米的正方形空地是八年级1﹣4班的卫生区，学校把它分成大小不同的四块，采用抽签的方式安排卫生区，下图是四个班级所抽到的卫生区情况，其中1班的卫生区是一块边长为（x﹣2y）米的正方形，其中0＜2y＜x．
（1）分别用x、y的式子表示八年3班和八年4班的卫生区的面积；
（2）求2班的卫生区的面积比1班的卫生区的面积多多少平方米？
参考答案：
【答案】（1）x2﹣4y2（2）8xy平方米
【解析】
试题分析：（1）结合图形、根据平方差公式计算即可；
（2）根据图形分别表示出2班的卫生区的面积和1班的卫生区，根据平方差公式和完全平方公式化简、求差即可．
解：（1）八年3班的卫生区的面积=（x﹣2y）[2x﹣（x﹣2y）]=x2﹣4y2；
八年4班的卫生区的面积=（x﹣2y）[2x﹣（x﹣2y）]=x2﹣4y2；
（2）[2x﹣（x﹣2y）]2﹣（x﹣2y）2=8xy．
答：2班的卫生区的面积比1班的卫生区的面积多8xy平方米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在等边△ABC中，点D是BC中点，点E在BA的延长线上，ED=EC，AC和ED交于点F，若AE=
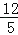，则CF= ．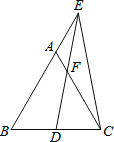
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个多边形的每个内角都等于140°，则这个多边形的边数是( )
A. 7 B. 8 C. 9 D. 10
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，直线BC与x轴、y轴分别交于B、C两点，直线AD与x轴，y轴分别交于A、D两点，其中A（﹣3，0）、B（4，0），C（0，4）并且AD⊥BC于点E
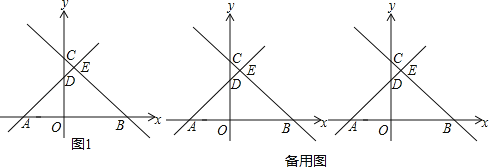
（1）求点D的坐标；
（2）点P从点A出发沿x轴正方向匀速运动，运动速度为每秒2个单位的长度，过点P作PM⊥x轴分别交直线AD、BC于点M、N，设点P的运动时间为t（秒），MN=m（m＞0），请用含t的式子表示m，并说明理由（并直接写出t的取值范围）；
（3）在（2）的条件下，EK⊥x轴于点K，连接MK，作KQ⊥MK交直线BC于点Q，当S△KQB=
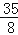时，求此时的P值及点M的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，AB为⊙O的直径，C为⊙O上一点，作AD⊥CD，垂足为D．
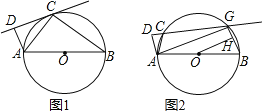
（1）若直线CD与⊙O相切于点C，求证：△ADC∽△ACB；
（2）如果把直线CD向下平行移动，如图2，直线CD交⊙O于C、G两点，若题目中的其他条件不变，tan∠DAC=
，AB=10，求圆心O到GB的距离OH的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】下列计算正确的是（ ）.
A．a3+a2=a5
B．a6÷a2=a3
C．（﹣3a2）2a3=﹣6a6
D．（﹣ab﹣1）2=a2b2+2ab+1
-
科目： 来源： 题型：
查看答案和解析>>【题目】A、B坐标分别为A（1,0）、B（0,2），若将线段AB平移到A1B1,A与A1对应，A1、B1的坐标分别为A1（2，a），B1（（b，3），则a+b= ___________ 。
相关试题
