【题目】如图,抛物线y=ax2+bx+3经过A(﹣3,0),B(﹣1,0)两点.
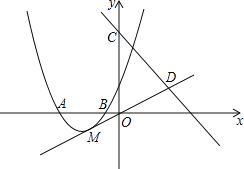
(1)求抛物线的解析式;
(2)设抛物线的顶点为M,直线y=﹣2x+9与y轴交于点C,与直线OM交于点D.现将抛物线平移,保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)只有一个公共点,求它的顶点横坐标的值或取值范围.
参考答案:
【答案】(1)y=x2+4x+3;(2)h=4,顶点横坐标的取值范围是![]() ≤h<
≤h<![]() 或h=4.
或h=4.
【解析】
试题分析:(1)直接用待定系数法就可以求出抛物线的解析式;
(2)由(1)的解析式求出抛物线的顶点坐标,根据抛物线的顶点坐标求出直线OD的解析式,设平移后的抛物线的顶点坐标为(h,![]() h),就可以表示出平移后的解析式,当抛物线经过点C时就可以求出h值,抛物线与直线CD只有一个公共点时可以得出
h),就可以表示出平移后的解析式,当抛物线经过点C时就可以求出h值,抛物线与直线CD只有一个公共点时可以得出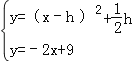 ,得x2+(﹣2h+2)x+h2+
,得x2+(﹣2h+2)x+h2+![]() h﹣9=0,从而得出△=(﹣2h+2)2﹣4(h2+
h﹣9=0,从而得出△=(﹣2h+2)2﹣4(h2+![]() h﹣9)=0求出h=4,从而得出结论.
h﹣9)=0求出h=4,从而得出结论.
解:(1)抛物线解析式y=ax2+bx+3经过A(﹣3,0),B(﹣1,0)两点,
∴![]() ,
,
解得![]() ,
,
∴抛物线的解析式为y=x2+4x+3.
(2)由(1)配方得y=(x+2)2﹣1,
∴抛物线的顶点坐标为M(﹣2,﹣1),
∴直线OD的解析式为y=![]() x,
x,
于是可设平移后的抛物线的顶点坐标为(h,![]() h),
h),
∴平移后的抛物线的解析式为y=(x﹣h)2+![]() h,
h,
当抛物线经过点C时,∵C(0,9),
∴h2+![]() h=9.
h=9.
解得h=![]() ,
,
∴当![]() ≤h<
≤h<![]() 时,平移后的抛物线与射线CD只有一个公共点;
时,平移后的抛物线与射线CD只有一个公共点;
当抛物线与直线CD只有一个公共点时,
由方程组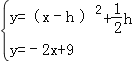 ,
,
得x2+(﹣2h+2)x+h2+![]() h﹣9=0,
h﹣9=0,
∴△=(﹣2h+2)2﹣4(h2+![]() h﹣9)=0,
h﹣9)=0,
解得h=4,
此时抛物线y=(x﹣4)2+2与直线CD唯一的公共点为(3,3),点(3,3)在射线CD上,符合题意.
故平移后抛物线与射线CD只有一个公共点时,顶点横坐标的取值范围是![]() ≤h<
≤h<![]() 或h=4.
或h=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是( )
A.n个 B.(n-1)个 C.(n-2)个 D.(n-3)个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=BC,以AB为直径的圆O交AC于点D,过点D作DE⊥BC,垂足为E,连接OE.
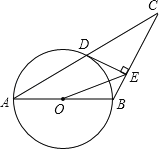
(1)求证:DE是⊙O的切线;
(2)若CD=
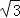 ,∠ACB=30°,求OE的长.
,∠ACB=30°,求OE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
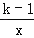 (k为常数,k≠1).
(k为常数,k≠1).(1)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(2)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(3)若其图象的一支位于第二象限,在这一支上任取两点A(x1、x2)、B(x2、y2),当y1>y2时,试比较x1与x2的大小;
(4)若在其图象上任取一点,向x轴和y轴作垂线,若所得矩形面积为6,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数a<b,则下列结论中,不正确的是( )
A. 4a<4b B. a+4<b+4 C. -4a<-4b D. a-4<b-4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中具有稳定性的是( )
A. 正方形 B. 直角三角形 C. 长方形 D. 平行四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(﹣2,1)是平面直角坐标系中的一点,将点P向左平移3个单位长度,再向下平移4个单位长度,得到点P′的坐标是_________.
相关试题

