【题目】如图,已知△ABC中,AB=BC,以AB为直径的圆O交AC于点D,过点D作DE⊥BC,垂足为E,连接OE.
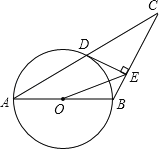
(1)求证:DE是⊙O的切线;
(2)若CD=![]() ,∠ACB=30°,求OE的长.
,∠ACB=30°,求OE的长.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OD、BD,求出BD⊥AC,AD=DC,根据三角形的中位线得出OD∥BC,推出OD⊥DE,根据切线的判定推出即可;
(2)解直角三角形求出BC、BD,求出AB得出OD,根据三角形的面积公式求出高DE,在△ODE中,根据勾股定理求出OE即可.
(1)证明:连接OD、BD,
∵AB是⊙O直径,
∴∠ADB=90°,
∴BD⊥AC,
∵AB=BC,
∴D为AC中点,
∵OA=OB,
∴OD∥BC,
∵DE⊥BC,
∴DE⊥OD,
∵OD为半径,
∴DE是⊙O的切线;
(2)解:∵CD=![]() ,∠ACB=30°,
,∠ACB=30°,
∴cos30°=![]() ,
,
∴BC=2,
∴BD=![]() BC=1,
BC=1,
∵AB=BC,
∴∠A=∠C=30°,
∵BD=1,
∴AB=2BD=2,
∴OD=1,
在Rt△CDB中,由三角形面积公式得:BC×DE=BD×CD,
1×![]() =2DE,
=2DE,
DE=![]() ,
,
在Rt△ODE中,由勾股定理得:OE=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列正多边形材料中,不能单独用来铺满地面的是( )
(A)正三角形 (B)正四边形 (C)正五边形 (D)正六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明去超市买东西花20元,他身上只带了面值为2元和5元的纸币,营业员没有零钱找给他,那么小明付款方式有( ).
A.2种 B.3种 C.4种 D.5种
-
科目: 来源: 题型:
查看答案和解析>>【题目】从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是( )
A.n个 B.(n-1)个 C.(n-2)个 D.(n-3)个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
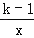 (k为常数,k≠1).
(k为常数,k≠1).(1)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(2)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(3)若其图象的一支位于第二象限,在这一支上任取两点A(x1、x2)、B(x2、y2),当y1>y2时,试比较x1与x2的大小;
(4)若在其图象上任取一点,向x轴和y轴作垂线,若所得矩形面积为6,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+3经过A(﹣3,0),B(﹣1,0)两点.
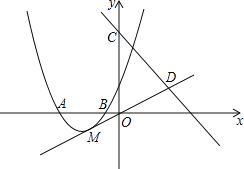
(1)求抛物线的解析式;
(2)设抛物线的顶点为M,直线y=﹣2x+9与y轴交于点C,与直线OM交于点D.现将抛物线平移,保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)只有一个公共点,求它的顶点横坐标的值或取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数a<b,则下列结论中,不正确的是( )
A. 4a<4b B. a+4<b+4 C. -4a<-4b D. a-4<b-4
相关试题

