搜索
【题目】如图，△ABC为等边三角形，点D，E分别在AC，BC上，且AD＝CE，AE与BD相交于点P，BF⊥AE于点F．若PF＝2，则BP＝（ ）
A. 3 B. 4 C. 5 D. 6
参考答案：
【答案】B
【解析】
首先证△ABD≌△CAE，推出∠ABD=∠CAE，求出∠BPF=∠APD=60°，得出∠PBF=30°，根据含30度角的直角三角形性质求出BP=2PF即可．
∵△ABC是等边三角形，.
∴AB=AC，.
∠BAC=∠C，.
在△ABD和△CAE中，
，.
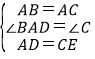∴△ABD≌△CAE，.
∴∠ABD=∠CAE，.
∴∠APD=∠ABP+∠PAB=∠BAC=60°，.
∴∠BPF=∠APD=60°，.
在Rt△BFP中，∠PBF=30°，.
∴BP=2PF，
∵PF=2，
∴BP=4.
故选B.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直角坐标平面内，已知点
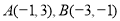，将点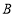
向右平移5个单位得到点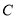
(1)描出点
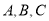的位置，并求
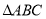的面积．(2)若在
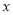轴下方有一点
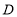，使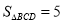
，写出一个满足条件的点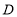的坐标．并指出满足条件的点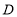有什么特征．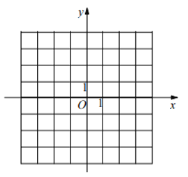
-
科目： 来源： 题型：
查看答案和解析>>【题目】根据要求回答问题：
（1）【提出问题】
已知：菱形ABCD的变长为4，∠ADC=60°，△PEF为等边三角形，当点P与点D重合，点E在对角线AC上时（如图1所示），求AE+AF的值；
（2）【类比探究】
在上面的问题中，如果把点P沿DA方向移动，使PD=1，其余条件不变（如图2），你能发现AE+AF的值是多少？请直接写出你的结论；
（3）【拓展迁移】
在原问题中，当点P在线段DA的延长线上，点E在CA的延长线上时（如图3），设AP=m，则线段AE、AF的长与m有怎样的数量关系？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】把正方体的6个面分别涂上不同的颜色，并画上朵数不等的花，各面上的颜色与花朵数的情况如下表：
颜色
红
黄
蓝
白
紫
绿
花朵数
1
2
3
4
5
6
现将上述大小相同，颜色、花朵分布完全一样的四个正方体拼成一个在同一平面上放置的长方体，如图所示，那么长方体的下底面共有_____朵花．
-
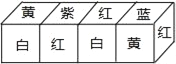
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）.
(1) 请画出△ABC向左平移5个单位长度后得到的△A
B
C
；(2) 请画出△ABC关于原点对称的△A
B
C
；(3) 在
轴上求作一点P，使△PAB的周长最小，请画出△PAB，并直接写出P的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，AD⊥BC于点D，AE是∠BAC的平分线，∠B＝30°，∠C＝70°，分别求：
（1）∠BAC的度数；
（2）∠AED的度数；
（3）∠EAD的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知下列命题中为真命题的是（ ）
①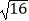
的算术平方根是4；
②若ma2＞na2 ， 则m＞n；
③正八边形的一个内角的度数是135°；
④对角线互相垂直平分的四边形是菱形；
⑤平分弦的直径垂直于弦．
A.①③④
B.②③⑤
C.①④⑤
D.②③④
相关试题
