【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C,且B(1,0),C(0,3),将△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.
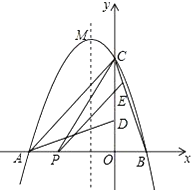
(1)求该二次函数的解析式;
(2)若点P为线段AB上的任一动点,过点P作PE∥AC,交BC于点E,连结CP,求△PCE面积S的最大值;
(3)设抛物线的顶点为M,Q为它的图象上的任一动点,若△OMQ为以OM为底的等腰三角形,求Q点的坐标.
参考答案:
【答案】(1)y=﹣x2﹣2x+3(2)![]() (3)Q(
(3)Q(![]() ,
,![]() ),或(
),或(![]() ,
,![]() )
)
【解析】试题分析:(1)根据题意求出A、B、C的坐标,然后根据待定系数法求函数的解析式即可;
(2)设点P(x,0),则PB=1﹣x,根据三角形的面积可得二次函数的解析式,然后根据二次函数的最值可求解;
(3)根据配方法求出顶点的坐标,然后根据等腰三角形的性质,结合勾股定理列方程可求解.
试题解析:(1)∵B(1,0),C(0,3),∴OB=1,OC=3.
∵△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.
∴OA=OC=3,∴A(﹣3,0),
∵点A,B,C在抛物线上,
∴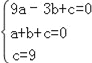 ,∴
,∴ ,∴二次函数的解析式为y=﹣x2﹣2x+3,
,∴二次函数的解析式为y=﹣x2﹣2x+3,
(2)设点P(x,0),则PB=1﹣x,
∴S△PBE=![]() (1﹣x)2,
(1﹣x)2,
∴S△PCE=S△PBC﹣S△PBE=![]() PB×OC﹣
PB×OC﹣![]() (1﹣x)2=
(1﹣x)2=![]() (1﹣x)×3﹣
(1﹣x)×3﹣![]() (1﹣x)2=﹣
(1﹣x)2=﹣![]() (x﹣1)2+
(x﹣1)2+![]() ,
,
当x=1时,S△PCE的最大值为![]() .
.
(3)∵二次函数的解析式为y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴顶点坐标(﹣1,4),
∵△OMQ为等腰三角形,OM为底,
∴MQ=OQ,
∴![]() =
=![]() ,
,
∴8x2+18x=7=0,∴x=![]() ,∴y=
,∴y=![]() 或y=
或y=![]() ,
,
∴Q(![]() ,
,![]() ),或(
),或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程ax2+bx+c=0是一元二次方程,则满足( )
A.a≠0B.a>0C.a≥0D.全体实数
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.x7+x2=x9
B.x12÷x6=x2
C.x2×x3=x6
D.(﹣x3)2=x6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:
 ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度数等于 度;
(2)求山坡A、B两点间的距离(结果精确到0.1米).
(参考数据:
 ≈1.414,
≈1.414, ≈1.732)
≈1.732) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,A(0,4),B(﹣3,0),C(2,0),D为B点关于AC的对称点,反比例函数y=
 的图象经过D点.
的图象经过D点.
(1)证明四边形ABCD为菱形;
(2)求此反比例函数的解析式;
(3)已知在y=
 的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.
的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】若正多边形的一个外角是45°,则该正多边形的边数是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+bx+a=0有一个根是﹣a(a≠0),则a﹣b的值为( )
A.a﹣b=1B.a﹣b=﹣1C.a﹣b=0D.a﹣b=±1
相关试题

