【题目】求证:两边分别相等且其中一组等边的对角相等的两个锐角三角形全等.
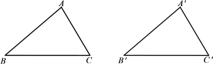
参考答案:
【答案】答案见解析
【解析】
画出图形,结合图形写出已知、求证,然后证明即可.
过点A作AD⊥BC于点D,过点A′ 作A′D′⊥B′C′于点D′,先证明△ACD≌△A′C′D′,得到AD= A′D′.再证明Rt△ABD≌Rt△A' B' D',得到∠B =∠B'.最后证明△ABC≌△A' B' C'即可.
已知:如图,在锐角三角形ABC和锐角三角形△A′B′C′中,AB=A′B′,AC= A′C′,∠C=∠C′.
求证:△ABC≌△A′B′C′.

证明:过点A作AD⊥BC于点D,过点A′ 作A′D′⊥B′C′于点D′,∴∠ADC=∠A′D′C′=∠ADB=∠A′D′B′=90°.
在△ACD和△A′C′D′中,∵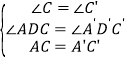 ,∴△ACD≌△A′C′D′(AAS),∴AD= A′D′.
,∴△ACD≌△A′C′D′(AAS),∴AD= A′D′.
在![]() △ABD和Rt△A′B′D′中,∵
△ABD和Rt△A′B′D′中,∵![]() ,∴Rt
,∴Rt![]() ≌Rt
≌Rt![]() (HL),∴∠
(HL),∴∠![]()
![]() ∠
∠![]() .
.
在△ABC和△A' B' C' 中,∵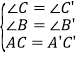 ,∴
,∴![]() ≌
≌![]() (AAS).
(AAS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
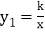 的图象与一次函数
的图象与一次函数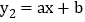 的图象交于点A(1,4)和点B
的图象交于点A(1,4)和点B(
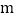 ,
,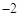 ).
).
(1)求这两个函数的表达式;
(2)观察图象,当
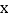 >0时,直接写出
>0时,直接写出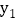 >
>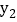 时自变量
时自变量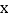 的取值范围;
的取值范围;(3)如果点C与点A关于
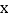 轴对称,求△ABC的面积.
轴对称,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的两条中线AD、BE交于点F,连接CF,若△ABC的面积为24,则△ABF的面积为( )

A. 10 B. 8 C. 6 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场11月初花费15 000元购进一批某品牌英语点读笔,因深受顾客喜爱,销售一空.该商场于12月初又花费24 000元购进一批同品牌英语点读笔,且所购数量是11月初的1.5倍,但每支进价涨了10元.
(1)求商场11月初购进英语点读笔多少支?
(2)11月份商场该品牌点读笔每支的售价是270元,若12月份购买的点读笔全部售完,且所获利润是11月份利润的1.2倍,求12月份该品牌点读笔每支的售价?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 ,
, .
.(1)当
 >0时,判断
>0时,判断 与0的关系,并说明理由;
与0的关系,并说明理由;(2)设
 .
.①当
 时,求
时,求 的值;
的值;②若
 是整数,求
是整数,求 的正整数值.
的正整数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
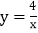 和
和 在第一象限内的图象如图所示,点
在第一象限内的图象如图所示,点 是
是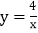 的图象上一动点,作
的图象上一动点,作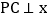 轴于点
轴于点 ,交
,交 的图象于点
的图象于点 ,作
,作 轴于点
轴于点 ,交
,交 的图象于点
的图象于点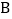 ,给出如下结论:①
,给出如下结论:①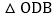 与
与 的面积相等;②
的面积相等;②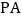 与
与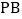 始终相等;③四边形
始终相等;③四边形 的面积大小不会发生变化;④
的面积大小不会发生变化;④ ,其中正确的结论序号是( )
,其中正确的结论序号是( )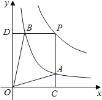
A. ①②③ B. ②③④ C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点M,O,N对应的数分别为﹣1,0,3,点P为数轴上任意点,其对应的数为x.

(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是: ;
(3)如果点P以每分钟2个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
相关试题

