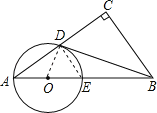
【题目】如图,在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
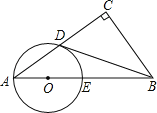
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
参考答案:
【答案】(1)见解析;(2)5.
【解析】
试题分析:(1)连接OD、DE,求出∠A=∠ADO,求出∠ADO+∠CDB=90°,求出∠ODB=90°,根据切线的判定推出即可;
(2)求出∠ADE=90°=∠C,推出BC∥DE,得出E为AB中点,推出AE=![]() AB,DE=
AB,DE=![]() BC=3,设AD=4a,AE=5a,由勾股定理求出DE=3a=3,求出a=1,求出AE即可.
BC=3,设AD=4a,AE=5a,由勾股定理求出DE=3a=3,求出a=1,求出AE即可.
(1)证明:连接OD、DE,
∵OA=OD,
∴∠A=∠ADO,
∵∠A+∠CDB=90°,
∴∠ADO+∠CDB=90°,
∴∠ODB=180°﹣90°=90°,
∴OD⊥BD,
∵OD是⊙O半径,
∴直线BD与⊙O相切;
(2)解:∵AE是⊙O直径,
∴∠ADE=90°=∠C,
∴BC∥DE,
∴△ADE∽△ACB,
∴![]() =
=![]()
∵D为AC中点,
∴AD=DC=![]() AC,
AC,
∴AE=BE=![]() AB,
AB,
DE是△ACB的中位线,
∴AE=![]() AB,DE=
AB,DE=![]() BC=
BC=![]() ×6=3,
×6=3,
设AD=4a,AE=5a,
在Rt△ADE中,由勾股定理得:DE=3a=3,
解得:a=1,
∴AE=5a=5,
答:⊙O的直径是5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=6cm,AC=8cm,BC=10cm,M是BC边上的动点,MD⊥AB,ME⊥AC,垂足分别是D、E,线段DE的最小值是 cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E,F分别为边AB,CD的中点,连接DE、BF、BD.
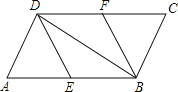
(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一腰上的高与另一腰的夹角为50°,则该三角形的顶角的度数为( )
A. 40° B. 50° C. 40°或140° D. 50°或140°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M.

(1)求证:DM=DA;
(2)如图②,点G在BE上,且∠BDG=∠C.求证:△DEG∽△ECF;
(3)在(2)的条件下,已知EF=2,CE=3,求GE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果⊙O的直径为6厘米,圆心O到直线AB的距离为6厘米,那么⊙O与直线AB的位置关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲布袋中有三个红球,分别标有数字1,2,3;乙布袋中有三个白球,分别标有数字2,3,4.这些球除颜色和数字外完全相同.小亮从甲袋中随机摸出一个红球,小刚从乙袋中随机摸出一个白球.
(1)用画树状图(树形图)或列表的方法,求摸出的两个球上的数字之和为6的概率;
(2)小亮和小刚做游戏,规则是:若摸出的两个球上的数字之和为奇数,小亮胜;否则,小刚胜.你认为这个游戏公平吗?为什么?
相关试题

