【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学就餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.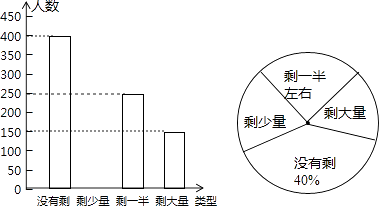
(1)这次被调查的同学共有名;
(2)补全条形统计图;
(3)计算在扇形统计图中剩大量饭菜所对应扇形圆心角的度数;
(4)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校20000名学生一餐浪费的食物可供多少人食用一餐?
参考答案:
【答案】
(1)1000
(2)解:如图所示
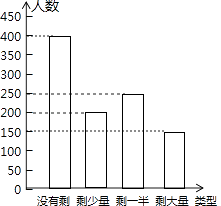
(3)解:在扇形统计图中剩大量饭菜所对应扇形圆心角的度数是:360°× ![]() =54°
=54°
(4)解: ![]() ×200=4000(人).
×200=4000(人).
答:校20000名学生一餐浪费的食物可供4000人食用一餐.
【解析】解:(1)被调查的同学的人数是400÷40%=1000(名);(2)剩少量的人数是1000﹣400﹣250﹣150=200(名),
(1)先根据没有剩饭的人数是400人,所占的百分比是40%,据此进行计算即可求得答案;
(2)利用(1)中求得结果减去其它组的人数即可求得剩少量饭的人数,再从而补全直方图即可;
(3)利用360°乘以对应的比例即可求解,剩大量饭菜所对应扇形圆心角的度数;
(4)利用20000除以调查的总人数,然后乘以200即可求解,即可得到学校20000名学生一餐浪费的食物可供多少人食用一餐.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,M是边AB的中点,CH⊥AB于点H,CD平分∠ACB.

(1)求证:∠1=∠2.
(2)过点M作AB的垂线交CD的延长线于点E,连结AE,BE.求证:CM=EM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )

A. (1,﹣1) B. (2,0) C. (﹣1,1) D. (﹣1,﹣1)
-
科目: 来源: 题型:
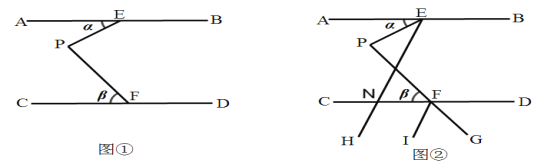
查看答案和解析>>【题目】如图①,已知AB∥CD,点E、F分别是AB、CD上的点,点P是两平行线之间的一点,设∠AEP=α,∠PFC=β,在图①中,过点E作射线EH交CD于点N,作射线FI,延长PF到G,使得PE、FG分别平分∠AEH、∠DFI,得到图②.
(1)在图①中,当α=20°,β=50°时,求∠EPF的度数;
(2)在(1)的条件下,求图②中∠END与∠CFI的度数;
(3)在图②中,当FI∥EH时,请求出α与β的数量关系.
-
科目: 来源: 题型:
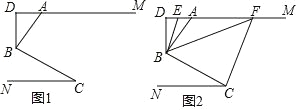
查看答案和解析>>【题目】如图 1,AM∥CN,点 B 为平面内一点,AB⊥BC 于 B,过 B 作 BD⊥ AM.
(1)求证:∠ABD=∠C;
(2)如图 2,在(1)问的条件下,分别作∠ABD、∠DBC 的平分线交 DM 于 E、F,若∠BFC=1.5∠ABF,∠FCB=2.5∠BCN,
①求证:∠ABF=∠AFB;
②求∠CBE 的度数.
-
科目: 来源: 题型:
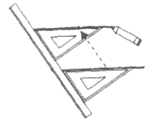
查看答案和解析>>【题目】如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是____________。
-
科目: 来源: 题型:
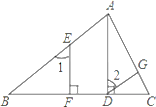
查看答案和解析>>【题目】完成下列证明:如图,已知AD⊥BC,EF⊥BC,∠1=∠2.
求证: DG∥BA.
证明:∵AD⊥BC,EF⊥BC ( 已知 )
∴∠EFB=90°,∠ADB=90°(_______________________ )
∴∠EFB=∠ADB ( 等量代换 )
∴EF∥AD ( _________________________________ )
∴∠1=∠BAD (________________________________________)
又∵∠1=∠2 ( 已知)
∴ (等量代换)
∴DG∥BA. (__________________________________)
相关试题

