Question

【题目】如图1，平面直角坐标系中，点A、B分别在x、y轴上，点B的坐标为（0，1），∠BAO＝30°，以AB为一边作等边△ABE，作OA的垂直平分线MN交AB的垂线AD于点D．

（1）写出点E的纵坐标．

（2）求证：BD＝OE；

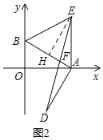
（3）如图2，连接DE交AB于F．求证：F为DE的中点．

Answer 1

【答案】（1）点E的纵坐标为2；（2）见解析；（3）见解析.

【解析】

（1）直接运用直角三角形30°角的性质和等边三角形的性质可得∠OAE＝90°，AE＝2；

（2）连接OD，易证△ADO为等边三角形，再证△ABD≌△AEO即可．

（3）作EH⊥AB于H，先证△ABO≌△AEH，得AO＝EH，再证△AFD≌△HFE即可．

（1）解：∵点B的坐标为（0，1），

∴OB＝1，

∵∠BAO＝30°，

Rt△ABO中，AB＝2OB＝2，

∵△ABE是等边三角形，

∴∠BAE＝60°，AE＝AB＝2，

∴∠OAE＝30°+60°＝90°，

∴点E的纵坐标为2；

故答案为：2；

（2）证明：连接OD，如图1，

∵△ABE是等边三角形，

∴AB＝BE，∠EAB＝60°，

∵DA⊥BA，

∴∠DAB＝90°，

∵∠BAO＝30°，

∴∠DAO＝90°﹣30°＝60°，

∴∠OAE＝∠DAB，

∵MN垂直平分OA，

∴OD＝DA，

∴△AOD是等边三角形，

∴DA＝OA，

在△ABD和△AEO中，

∵，

∴△ABD≌△AEO（SAS），

∴BD＝OE；

（3）证明：如图2，作EH⊥AB于H，

∴∠EHA＝∠DAF＝90°，

∵AE＝BE，

∴AH＝AB，

∵∠AOB＝90°，∠BAO＝30°，

∴OB＝AB，

∴AH＝BO，

∴Rt△AEH≌Rt△BAO（HL），

∴EH＝AO＝AD，

∵∠EHF＝∠DAF＝90°，∠EFH＝∠DFA，

∴△HFE≌△AFD（AAS），

∴EF＝DF，

∴F为DE的中点．